�Ȃ�������
< �ڎ��� >
�Ȑ���Ȗʂ��Ȃ��Ă���̂͒��ϓI�ɉ��邪�A��Ԃ��Ȃ��Ă���Ƃ����̂͂Ȃ��Ȃ��������ɂ������̂ł���B����𗝉�����ɂ͋ȗ��̐��w��A���R�ȋ�Ԃł̋Ȑ����W�n���w�сA�ȗ����`���A�������ʑ��ΐ����_�Ŏ�舵���l������ԂɓK�p����悢�B
�P. �ǁ@���@���@���@�n
���������ɂ��K���ȍ��W�n��I�Ԏ��ŁA�d�͂̑傫�����ǂ̂悤�ɂł��ς��鎖���o����B�Ⴆ�Ή����x���ŏ㏸���Ă��郍�P�b�g�̒��ł̏d�͂͒n���̏d�́{���ł���B���R�������Ă���G���x�[�^�̓����ł͏d�͂͑ł������ꖳ�d�͏�ԂɂȂ��Ă���B���̂悤�ɂ��ďd�͂�������������n���Ǐ������n�����Ǐ����[�����c�n�ƌĂԁB����̓G���x�[�^�̓����̏d�͂���l�ł��鎖�����肵�Ă���B�G���x�[�^�����̏d�͂����l�A���̕��������Ƃ���ƁA���̕��ɂ��镨�̂͏d�͂��������������̕��ɓ��������n�łȂ��Ȃ�B���̂悤�ɑ��I�Ȋ����n����鎖�͕s�\�ł���B�������ǂ�ȏd�͏�����ԂƋ�Ԃ̏\�������ȗ̈�ɂ킽���Ă͈�l�ƌ��Ȃ������o����B�]���Ă����Ǐ������n����鎖���o����B�����͉������ꂽ���q�̏u�ԓI���������n�i��MCR�n�j�ɗގ��������̂ł���B�d�͏�̔��l���͒��̊����������N�����B���̌������㐶����͂��͂ƌ����B�����n������l�ȏd�͏�̒��ɂ���A���̊����͋N����Ȃ��B���Ƒ��z�̏d�͏�̒n���̒��a�ɂ킽��Ⴂ�ɂ���Ē��̊������N����B
(1) �Ǐ����R��
�Ǐ������n�͓��R�Ǐ��I�ɕ��R�ł���B
���ꑊ�Θ_�ɉ�����~���R�t�X�L�[��Ԃ́A���[�N���b�h�w�̕��s���̌����ɏ]�����畽�R�Ȃł���B���������̃��g���b�N�����[�N���b�h����̂���Ƃ͈قȂ�̂Ń��[�N���b�h��Ԃł͂Ȃ��B���q�͌ŗL���[���̂܂������Ȑ��E������B�]���ē��ꑊ�Θ_�͕��R���[�N���b�h�w�ɏ]���B
���l�ȏd�͏�ł͕��s�ɓ����n�߂���̋ߐڂ������q�̐��E���͈�ʂɕ��s�ɂƂǂ܂��ĂȂ��B�]���ďd�͂̂��鎞��͕��R�łȂ��B���[�N���b�h�w�ŕ��s���̌����𗎂Ƃ��ƁA�Ȃ�����Ԃ�������B�Ⴆ�A���̕\�ʂ͋Ȃ��Ă���B���ʏ�ł̋Ǐ��I�Ȓ�����L���Ă����Ƒ�~�ɂȂ�A��̑�~�͕K�������B����ł��C�ӂ̓_�ɏ\���߂��͈͂ł͊w�͕��R�ł���ƌ��Ȃ������o����B��̊X�̒n�}�͈ꖇ�̎��̏�ɘc�݂Ȃ��ɕ`�������o����B�������n���S�̂ɂ��Ă��悤�Ƃ���Ύ��s����B���͂��̂悤���Ǐ��I�ɕ��R�ł���B
���ꑊ�Θ_�ɉ�����~���R�t�X�L�[��Ԃ́A���[�N���b�h�w�̕��s���̌����ɏ]�����畽�R�Ȃł���B���������̃��g���b�N�����[�N���b�h����̂���Ƃ͈قȂ�̂Ń��[�N���b�h��Ԃł͂Ȃ��B���q�͌ŗL���[���̂܂������Ȑ��E������B�]���ē��ꑊ�Θ_�͕��R���[�N���b�h�w�ɏ]���B
���l�ȏd�͏�ł͕��s�ɓ����n�߂���̋ߐڂ������q�̐��E���͈�ʂɕ��s�ɂƂǂ܂��ĂȂ��B�]���ďd�͂̂��鎞��͕��R�łȂ��B���[�N���b�h�w�ŕ��s���̌����𗎂Ƃ��ƁA�Ȃ�����Ԃ�������B�Ⴆ�A���̕\�ʂ͋Ȃ��Ă���B���ʏ�ł̋Ǐ��I�Ȓ�����L���Ă����Ƒ�~�ɂȂ�A��̑�~�͕K�������B����ł��C�ӂ̓_�ɏ\���߂��͈͂ł͊w�͕��R�ł���ƌ��Ȃ������o����B��̊X�̒n�}�͈ꖇ�̎��̏�ɘc�݂Ȃ��ɕ`�������o����B�������n���S�̂ɂ��Ă��悤�Ƃ���Ύ��s����B���͂��̂悤���Ǐ��I�ɕ��R�ł���B
(2) �Ǐ����R���̃��g���b�N�ɂ�鐔�w�I�\��
���ꑊ�Θ_�ł͎����R�ł������������������������ł��������A��ʑ��Θ_�ł͏�ŏq�ׂ��l�ɏd�͂����݂���ׂɁA���I�ɂ͂��������n�͑��݂��Ȃ��B�������Ǐ��I�ɂ����������������ƂȂ�n�����݂���B
���`�㐔�̂悭�m��ꂽ�藝�ɂ�������������������������Ƃ��鎖���\�ł���B �i�ڍׂ��t�^�P�F�����s��̑Ίp�s��ւ̕ϊ����Q��)
�@�@�@���@�������iP�j�������� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�j
P�̋ߖT�ł�����������̂��ꂪ�����ł��邽�߂ɂ�
�@�@�@���@���������iP�j�^�݂w�����O�@�\�\�� �@ �����������O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�j
��Ԃ������ɕ��R�łȂ����
�@�@�@���@��2�������iP�j�^�݂w���݂w ���� �O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�j
�Ǐ������n�����݂���Ƃ����̂́A�ǂ̂悤�ɋȂ�����Ԃł��A�C�ӂ̓_�ɂ����āA���̋�Ԃɐڂ��镽�R�ȋ�Ԃ����݂���Ƃ������ł���B�Ǐ������n�Ő��藧�e���\���������͈�ʂ̍��W�n�ł����藧�B�i��ʂ̍��W�n����Ǐ������n�ւ̃e���\���̐����̕ϊ��ŏؖ��ł���B�j
�y�Ǐ����R���̏ؖ��z
���`�㐔�̂悭�m��ꂽ�藝�ɂ�������������������������Ƃ��鎖���\�ł���B �i�ڍׂ��t�^�P�F�����s��̑Ίp�s��ւ̕ϊ����Q��)
�Ȃ�����ԏ�̔C�ӂ̓_P�����_�Ƃ�
�@�@�@�������i�w���j���������{�O[�i�w���j2]
�@�@�@���@�������iP�j�������� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�j
P�̋ߖT�ł�����������̂��ꂪ�����ł��邽�߂ɂ�
�@�@�@���@���������iP�j�^�݂w�����O�@�\�\�� �@ �����������O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�j
��Ԃ������ɕ��R�łȂ����
�@�@�@���@��2�������iP�j�^�݂w���݂w ���� �O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�j
�Ǐ������n�����݂���Ƃ����̂́A�ǂ̂悤�ɋȂ�����Ԃł��A�C�ӂ̓_�ɂ����āA���̋�Ԃɐڂ��镽�R�ȋ�Ԃ����݂���Ƃ������ł���B�Ǐ������n�Ő��藧�e���\���������͈�ʂ̍��W�n�ł����藧�B�i��ʂ̍��W�n����Ǐ������n�ւ̃e���\���̐����̕ϊ��ŏؖ��ł���B�j
�y�Ǐ����R���̏ؖ��z
��ʂ��������͏ꏊ�̕��G�Ȋ��ł���ׂ�������W���g���A������ϊ����g���Ĉ�ʍ��W�n��
�Ǐ������n�֕ϊ����Ȃ���Ȃ�Ȃ��B
�ϊ��s������_�o�i���̍��W���w��'�Ƃ���j�̉��Ńe�[���[�W�J����B
�@�@������'( )��������' (P) �{ (�w��'�[�w��'0)
)��������' (P) �{ (�w��'�[�w��'0)  �{
�{ (�w��'�[�w ��'0)(�w��'�[�w��'0)
(�w��'�[�w ��'0)(�w��'�[�w��'0) 
�@�@�@�@�@�@�@��������'(P) �{ (�w��'�[�w ��'0)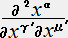 �{
�{ (�w��'�[�w��'0)(�w��'�[�w ��'0)
(�w��'�[�w��'0)(�w��'�[�w ��'0)  �@ �E�E�E�i�S�j
�@ �E�E�E�i�S�j
���l��
�@�@������'( )��������' (P) �{ (�w��'�[�w��'0)
)��������' (P) �{ (�w��'�[�w��'0) 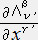 �{
�{ (�w��'�[�w ��'0)(�w��'�[�w��'0)
(�w��'�[�w ��'0)(�w��'�[�w��'0) 
�@�@�@�@�@�@�@��������'(P) �{ (�w��'�[�w ��'0)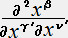 �{
�{ (�w��'�[�w��'0)(�w��'�[�w ��'0)
(�w��'�[�w��'0)(�w��'�[�w ��'0)  �@ �E�E�E�i�T�j
�@ �E�E�E�i�T�j
���l�Ƀ��g���b�N���e�[���[�W�J����
�@�@������( )��������(P) �{ (�w��'�[�w��'0)
)��������(P) �{ (�w��'�[�w��'0) 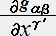 �{
�{ (�w��'�[�w��'0)(�w��'�[ �w��'0)
(�w��'�[�w��'0)(�w��'�[ �w��'0) 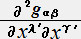 �@�@ �E�E�E�i�U�j
�@�@ �E�E�E�i�U�j
�ϊ�����
�@�@����'��'��������'������'���� ��
�i�S�j�C�i�T�j�C�i�U�j����̕ϊ����̉E�ӂɑ�������
�@�@����'��'( )�� ������'������'������ �{ (�w ��'�[�w��'0) ( ������'������'�������C��'
)�� ������'������'������ �{ (�w ��'�[�w��'0) ( ������'������'�������C��'
�@�@�@�@�@�@�@�@�@�@�@�{������'������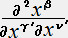 �{������'������
�{������'������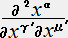 )
)
�@�@�@�@�@�@�@�@�@�@�@�{ (�w��'�[�w ��'0)(�w��'�[�w��'0) ( ������'������'�������C��'��'
(�w��'�[�w ��'0)(�w��'�[�w��'0) ( ������'������'�������C��'��'
�@�@�@�@�@�@�@�@�@�@�@�{������'������ �{������'������
�{������'������ )
)
�i�P�j�������́A���L�̎��������ł���B
�@�@�@����'��'��������'������'�� ����
��̎��������Ώ̂Ȃ̂Ń��ɂ��Ă�10�i��'���O�`�R�A��'����'�`�R�j�̘A���������ɂȂ�B���m������10�� �Ȃ̂ŏ�̎�������ϊ��s������'�����݂���B�̂Ɂi�P�j�����藧�B
�Ǐ������n�����݂���ɂ͂o�_�̋ߖT�ɂ����Ă����Ƃ̍��������łȂ���Ȃ�Ȃ��D���̂��߂����� �W�J���̂P���̍��i��(�w��'�[�w��'0)�̍��j���O�łȂ���Ȃ�Ȃ��B�܂艺�L�� �������藧���ł���B
�@�@�@������'������'�������C��'�{ ������'������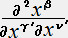 �{ ������'������
�{ ������'������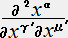 �� �O
�� �O
��̎��ɂ����ā@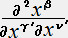 �� �O �C
�� �O �C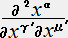 �� �O�@�Ȃ�@������'������'�� �����C��' �� �O �ł���B
�� �O�@�Ȃ�@������'������'�� �����C��' �� �O �ł���B
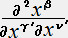 �� �O �� ������'���� ��'�������C��' �� �O ���S�O���̎��ł���B
�]����
�� �O �� ������'���� ��'�������C��' �� �O ���S�O���̎��ł���B
�]���� 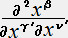 �� ������'�C��' �� �O �C
�� ������'�C��' �� �O �C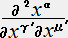 �� �O�@�ƌ��߂�i�Q�j�����藧�B
�� �O�@�ƌ��߂�i�Q�j�����藧�B
�Q���̍��ɉ����āA�P�O�O���̎�����'��'�C��'��' �� �O ���� ��悤�ɁA����'��'�C��'��'�����߂鎖�͏o���Ȃ��B���̂Ȃ烩��'��'�C ��'��'���W�O���ł��邩��A�W�O�̂Q�K�����͏��������o���邪�A�Q�O�̂Q�K�����͏������� �o���Ȃ��B�]���āi�R�j�����藧�B���R�ȋ�Ԃł͑S�Ă��O�ɂȂ�B
�ϊ��s������_�o�i���̍��W���w��'�Ƃ���j�̉��Ńe�[���[�W�J����B
�@�@������'(
 )��������' (P) �{ (�w��'�[�w��'0)
)��������' (P) �{ (�w��'�[�w��'0)  �{
�{ (�w��'�[�w ��'0)(�w��'�[�w��'0)
(�w��'�[�w ��'0)(�w��'�[�w��'0) 
�@�@�@�@�@�@�@��������'(P) �{ (�w��'�[�w ��'0)
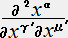 �{
�{ (�w��'�[�w��'0)(�w��'�[�w ��'0)
(�w��'�[�w��'0)(�w��'�[�w ��'0)  �@ �E�E�E�i�S�j
�@ �E�E�E�i�S�j���l��
�@�@������'(
 )��������' (P) �{ (�w��'�[�w��'0)
)��������' (P) �{ (�w��'�[�w��'0) 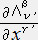 �{
�{ (�w��'�[�w ��'0)(�w��'�[�w��'0)
(�w��'�[�w ��'0)(�w��'�[�w��'0) 
�@�@�@�@�@�@�@��������'(P) �{ (�w��'�[�w ��'0)
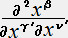 �{
�{ (�w��'�[�w��'0)(�w��'�[�w ��'0)
(�w��'�[�w��'0)(�w��'�[�w ��'0)  �@ �E�E�E�i�T�j
�@ �E�E�E�i�T�j���l�Ƀ��g���b�N���e�[���[�W�J����
�@�@������(
 )��������(P) �{ (�w��'�[�w��'0)
)��������(P) �{ (�w��'�[�w��'0) 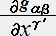 �{
�{ (�w��'�[�w��'0)(�w��'�[ �w��'0)
(�w��'�[�w��'0)(�w��'�[ �w��'0) 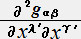 �@�@ �E�E�E�i�U�j
�@�@ �E�E�E�i�U�j�ϊ�����
�@�@����'��'��������'������'���� ��
�i�S�j�C�i�T�j�C�i�U�j����̕ϊ����̉E�ӂɑ�������
�@�@����'��'(
 )�� ������'������'������ �{ (�w ��'�[�w��'0) ( ������'������'�������C��'
)�� ������'������'������ �{ (�w ��'�[�w��'0) ( ������'������'�������C��'�@�@�@�@�@�@�@�@�@�@�@�{������'������
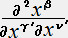 �{������'������
�{������'������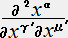 )
)�@�@�@�@�@�@�@�@�@�@�@�{
 (�w��'�[�w ��'0)(�w��'�[�w��'0) ( ������'������'�������C��'��'
(�w��'�[�w ��'0)(�w��'�[�w��'0) ( ������'������'�������C��'��'�@�@�@�@�@�@�@�@�@�@�@�{������'������
 �{������'������
�{������'������ )
)�i�P�j�������́A���L�̎��������ł���B
�@�@�@����'��'��������'������'�� ����
��̎��������Ώ̂Ȃ̂Ń��ɂ��Ă�10�i��'���O�`�R�A��'����'�`�R�j�̘A���������ɂȂ�B���m������10�� �Ȃ̂ŏ�̎�������ϊ��s������'�����݂���B�̂Ɂi�P�j�����藧�B
�Ǐ������n�����݂���ɂ͂o�_�̋ߖT�ɂ����Ă����Ƃ̍��������łȂ���Ȃ�Ȃ��D���̂��߂����� �W�J���̂P���̍��i��(�w��'�[�w��'0)�̍��j���O�łȂ���Ȃ�Ȃ��B�܂艺�L�� �������藧���ł���B
�@�@�@������'������'�������C��'�{ ������'������
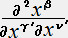 �{ ������'������
�{ ������'������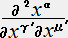 �� �O
�� �O��̎��ɂ����ā@
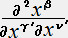 �� �O �C
�� �O �C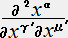 �� �O�@�Ȃ�@������'������'�� �����C��' �� �O �ł���B
�� �O�@�Ȃ�@������'������'�� �����C��' �� �O �ł���B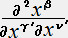 �� �O �� ������'���� ��'�������C��' �� �O ���S�O���̎��ł���B
�]����
�� �O �� ������'���� ��'�������C��' �� �O ���S�O���̎��ł���B
�]���� 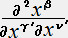 �� ������'�C��' �� �O �C
�� ������'�C��' �� �O �C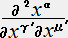 �� �O�@�ƌ��߂�i�Q�j�����藧�B
�� �O�@�ƌ��߂�i�Q�j�����藧�B�Q���̍��ɉ����āA�P�O�O���̎�����'��'�C��'��' �� �O ���� ��悤�ɁA����'��'�C��'��'�����߂鎖�͏o���Ȃ��B���̂Ȃ烩��'��'�C ��'��'���W�O���ł��邩��A�W�O�̂Q�K�����͏��������o���邪�A�Q�O�̂Q�K�����͏������� �o���Ȃ��B�]���āi�R�j�����藧�B���R�ȋ�Ԃł͑S�Ă��O�ɂȂ�B
�Q. ���@�ρ@���@��
�Ǐ������n�͋Ǐ��I�ɂ͑S�Ă����ꑊ�Θ_�I�ł���n�ł���A�����̊��x�N�g���̔����̓[���ł���B�]���ăx�N�g�� �̋��ϔ����́A�N���X�g�b�t�F���L���������āA�P�Ȃ鐬���̕Δ����ŗ^������B����
�@�@�@�u���G�����u���C���@ �@�@�@�@�@�@�i���̌n�̓_�o�Łj
�@�@�@�����G���������C�����O�@�@�@�@�@�i�_�o�Łj
�����G�����O�@�̓e���\���������Ȃ̂ň�ʂ̍��W�n�ł����藧�B
�Ȃ�����Ԃ̔C�ӂ̍��W�n�ł�
�@�@�@���@������������������ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�V�j
�@�@�@���@�����ʃ��� ������ �i ������,���{������,���[���ʃ�,�� �j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�W�j
������ �i ������,���{������,���[���ʃ�,�� �j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�W�j
�@�@�@���@�u���G�����u���C���{�����ʃ��u �� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�X�j
�@�@�@���@�o���G�����o���C���[���������o�� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�O�j
�@�@�@���@�s�����G�����s�����C���{�����ʃ��s �ʃ��{�����ʃ��s���� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�P�j
�����藧�B�@�i�Ȑ����W�n�́@�V. ���@�ρ@���@�� �� �X. �N���X�g�b�t�F�� �L���ƃ��g���b�N���Q�Ɓj
�Ǐ������n�ł� �����������O �ł��邪�A���̌n�ł̓_�o�ɉ����� �������� �̔����� ������,�ʃ� ���܂ނ̂ň�ʂɂ� �S�����[���ɂ͂Ȃ�Ȃ��B�����������R�Ȃ� �������� �̔����̓[���ł���B�Ȃ� ����Ԃƕ��R�ȋ�ԂƂ̈Ⴂ�́A�C�ӂ̓_�ł̃N���X�g�b�t�F���L���̔����i�����g���b�N�̂Q������j�Ɍ����B
�y���U�̌����z
�@�@�@�u���G�����u���C���@ �@�@�@�@�@�@�i���̌n�̓_�o�Łj
�@�@�@�����G���������C�����O�@�@�@�@�@�i�_�o�Łj
�����G�����O�@�̓e���\���������Ȃ̂ň�ʂ̍��W�n�ł����藧�B
�Ȃ�����Ԃ̔C�ӂ̍��W�n�ł�
�@�@�@���@������������������ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�V�j
�@�@�@���@�����ʃ���
 ������ �i ������,���{������,���[���ʃ�,�� �j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�W�j
������ �i ������,���{������,���[���ʃ�,�� �j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�W�j�@�@�@���@�u���G�����u���C���{�����ʃ��u �� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�X�j
�@�@�@���@�o���G�����o���C���[���������o�� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�O�j
�@�@�@���@�s�����G�����s�����C���{�����ʃ��s �ʃ��{�����ʃ��s���� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�P�j
�����藧�B�@�i�Ȑ����W�n�́@�V. ���@�ρ@���@�� �� �X. �N���X�g�b�t�F�� �L���ƃ��g���b�N���Q�Ɓj
�Ǐ������n�ł� �����������O �ł��邪�A���̌n�ł̓_�o�ɉ����� �������� �̔����� ������,�ʃ� ���܂ނ̂ň�ʂɂ� �S�����[���ɂ͂Ȃ�Ȃ��B�����������R�Ȃ� �������� �̔����̓[���ł���B�Ȃ� ����Ԃƕ��R�ȋ�ԂƂ̈Ⴂ�́A�C�ӂ̓_�ł̃N���X�g�b�t�F���L���̔����i�����g���b�N�̂Q������j�Ɍ����B
�y���U�̌����z
�C�ӂ̃x�N�g���ꂪ�^����ꂽ���A���̔��U�͉��L�̎��ɂȂ�B
�@�@�@�u���G�����u���C���{�����ʃ��u ��
��̎��ɂ̓N���X�g�b�t�F���L���̂Ƃ���ɘa���܂܂�Ă���
�@�@�@�����ʃ��� �������i ������,���{������,���[���ʃ�,�� �j
�������i ������,���{������,���[���ʃ�,�� �j
�@�@�@�@�@�@�@�@�� ������������,���[
������������,���[ ���������ʃ�,���{
���������ʃ�,���{ ������������,��
������������,��
�ƂȂ�B��P���̃_�~�[�̓Y�����ƃ����@���[�[�����@�C���[�[���Ё@��
��Q���̃_�~�[�̓Y�����ƃ����@���[�[���Ё@�C���[�[�����ɂ��ꂼ�ꏑ���������
�@�@�@�����ʃ��� ������������,��
������������,��
�s��i�������j�̍s�����Ƃ���B���̔�����
�@�@�@���C������������������,���@�@�i�t�^�S�F�s�̔������Q�Ɓj
�]����
�@�@�@���@�����ʃ������C���^�Q�����i
 �j�C���^�Q�����i
�j�C���^�Q�����i �j�C���^
�j�C���^ �@�E�E�E�E�E�E�E�E�E�@�i�P�Q�j
�̂�
�@�E�E�E�E�E�E�E�E�E�@�i�P�Q�j
�̂�
�@�@�@���@�u���G�����u���C���{�u���i �j�C���^
�j�C���^ ���i
���i �u���j�C���^
�u���j�C���^ �@�@�E�E�E�E�E�E�E�E�E�@�i�P�R�j
�@�@�E�E�E�E�E�E�E�E�E�@�i�P�R�j
�s�����̒l�����Ȃ������[���Œu��������B �Ȑ����W�n�@�W. ���U�ƃ��v���V�A���ŋ��߂��ɍ��W�ɉ����锭�U�Ə�̎��ł̔��U�Ƃ��ׂĂ݂�B
�s��������2 ������ �����B�������̎��ɑ�������
�����B�������̎��ɑ�������
�@�@�@�u��;�����i���u���j�C���^����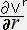 �{
�{ 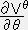 �{
�{  �u�� ��
�u�� �� 
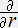 �i���u�� �j �{
�i���u�� �j �{ 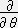 �u���@
�u���@
����Ɍv�Z�����̂ƈ�v����B ��`���̔��U�͏�̎��̂u���̑���ɁA���g���b�N���g���Ĉ�`���i�����z�j���ʑ������x�N�g�����z���g�p����B
�@�@�@���@�u���G�����i ���������C���j�C���^
���������C���j�C���^ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�S�j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�S�j
�ɍ��W�ł̈�`���̔��U����̎����g���ċ��߂��
�@�@�@�u���G�����i ���Cr�j�Cr�^
���Cr�j�Cr�^ �{�i
�{�i ���C���^��2�j�C���^
���C���^��2�j�C���^
�@�@�@�@�@�@�@ ���i�����Cr�j�Cr�^���{�i���C���^��>�j�C���^��
�@�@�@�@�@�@�@ ��
 �{
�{ 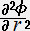 �{
�{

����Ɍv�Z�����̂ƈ�v����B
�e���\�����s�̔��U�͉��L�̎��ɂȂ�B
�@�@�@���@�s�����G�����s�����C���{�����ʃ��s �ʃ��{�����ʃ��s���� �@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�T�j
�@�@�@�u���G�����u���C���{�����ʃ��u ��
��̎��ɂ̓N���X�g�b�t�F���L���̂Ƃ���ɘa���܂܂�Ă���
�@�@�@�����ʃ���
 �������i ������,���{������,���[���ʃ�,�� �j
�������i ������,���{������,���[���ʃ�,�� �j�@�@�@�@�@�@�@�@��
 ������������,���[
������������,���[ ���������ʃ�,���{
���������ʃ�,���{ ������������,��
������������,���ƂȂ�B��P���̃_�~�[�̓Y�����ƃ����@���[�[�����@�C���[�[���Ё@��
��Q���̃_�~�[�̓Y�����ƃ����@���[�[���Ё@�C���[�[�����ɂ��ꂼ�ꏑ���������
�@�@�@�����ʃ���
 ������������,��
������������,���s��i�������j�̍s�����Ƃ���B���̔�����
�@�@�@���C������������������,���@�@�i�t�^�S�F�s�̔������Q�Ɓj
�]����
�@�@�@���@�����ʃ������C���^�Q�����i

 �j�C���^�Q�����i
�j�C���^�Q�����i �j�C���^
�j�C���^ �@�E�E�E�E�E�E�E�E�E�@�i�P�Q�j
�̂�
�@�E�E�E�E�E�E�E�E�E�@�i�P�Q�j
�̂��@�@�@���@�u���G�����u���C���{�u���i
 �j�C���^
�j�C���^ ���i
���i �u���j�C���^
�u���j�C���^ �@�@�E�E�E�E�E�E�E�E�E�@�i�P�R�j
�@�@�E�E�E�E�E�E�E�E�E�@�i�P�R�j�s�����̒l�����Ȃ������[���Œu��������B �Ȑ����W�n�@�W. ���U�ƃ��v���V�A���ŋ��߂��ɍ��W�ɉ����锭�U�Ə�̎��ł̔��U�Ƃ��ׂĂ݂�B
�s��������2 ������
 �����B�������̎��ɑ�������
�����B�������̎��ɑ��������@�@�@�u��;�����i���u���j�C���^����
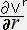 �{
�{ 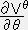 �{
�{  �u�� ��
�u�� �� 
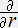 �i���u�� �j �{
�i���u�� �j �{ 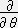 �u���@
�u���@����Ɍv�Z�����̂ƈ�v����B ��`���̔��U�͏�̎��̂u���̑���ɁA���g���b�N���g���Ĉ�`���i�����z�j���ʑ������x�N�g�����z���g�p����B
�@�@�@���@�u���G�����i
 ���������C���j�C���^
���������C���j�C���^ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�S�j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�S�j�ɍ��W�ł̈�`���̔��U����̎����g���ċ��߂��
�@�@�@�u���G�����i
 ���Cr�j�Cr�^
���Cr�j�Cr�^ �{�i
�{�i ���C���^��2�j�C���^
���C���^��2�j�C���^
�@�@�@�@�@�@�@ ���i�����Cr�j�Cr�^���{�i���C���^��>�j�C���^��
�@�@�@�@�@�@�@ ��

 �{
�{ 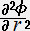 �{
�{

����Ɍv�Z�����̂ƈ�v����B
�e���\�����s�̔��U�͉��L�̎��ɂȂ�B
�@�@�@���@�s�����G�����s�����C���{�����ʃ��s �ʃ��{�����ʃ��s���� �@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�T�j
�R. ���@�s�@�ځ@��
�x�N�g���u��_�o����ڋ߂����p�ֈړ����������A�Ǐ������n�ɂ�����x�N�g���u�̐������ς��Ȃ����A����s�ړ��ł���Ƃ����B�ǂ̗l�ɋȂ�����Ԃł��C�ӂ̓_�ɂ����Ă��̋�Ԃɐڂ��镽�R�ȋ�Ԃ�����̂ł��̋�ԏ�ŕ��s�ړ����s���悢�B

��ŏq�ׂ����s�ړ��𐔎��ŕ\���B
�x�N�g���� �����}�̗l�ɂ���Ȑ���̊e�_�Œ�`����Ă���B
�����}�̗l�ɂ���Ȑ���̊e�_�Œ�`����Ă���B
�x�N�g�� ��
��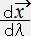 �͋Ȑ��ɐڂ���x�N�g���ł���B�i
�͋Ȑ��ɐڂ���x�N�g���ł���B�i 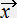 �͋Ȑ��̈ʒu�x�N�g���B�ɂ͋Ȑ��ɉ� �����p�����[�^�[ �j
�͋Ȑ��̈ʒu�x�N�g���B�ɂ͋Ȑ��ɉ� �����p�����[�^�[ �j
�@�@�@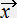 ���i�w0�C�w1�C�w2�C�w 3�j
���i�w0�C�w1�C�w2�C�w 3�j
�@�@�@ ���i
���i  �C
�C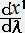 �C
�C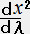 �C
�C �j
�j
�@�@�@ ��
��
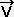 �����s�ړ��̎��A�Ǐ������n�ł͓_�o�ł�
�����s�ړ��̎��A�Ǐ������n�ł͓_�o�ł� 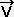 �� �����͋Ȑ��ɉ����Ĉ��łȂ��Ă͂Ȃ�Ȃ��B����
�� �����͋Ȑ��ɉ����Ĉ��łȂ��Ă͂Ȃ�Ȃ��B����
�@�@�@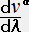 ���O
���O
�����������
�@�@�@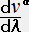 ���t���u���C��=�t ���u���G�����O
���t���u���C��=�t ���u���G�����O
�t���u���G�����O�����藧�̂́A�Ǐ������n�ł̓N���X�g�b�t�F���L���i���� ���ʃ��j���O������ł���B
�̂ɕ��s�ړ��̏����Ƃ���
�@�@�@���@�t���u���G�����O�@�@ �@�@ �u���G�����O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�U�j
�@�@ �u���G�����O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�U�j
�u���G�����O �̓e���\���������Ȃ̂ň�ʂ̌n�ł����藧���ł���B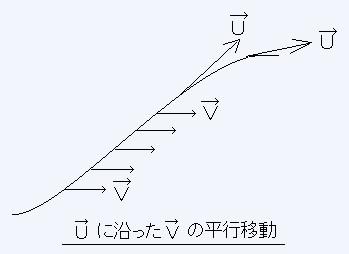

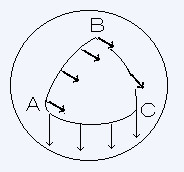
���ɕ��R�ȋ�Ԓ��ŋȐ��ɂ���č��ꂽ�O�p�`�̕����o�H���`����Ă���B�`����o�����āA�����O�̓_�ł̃x�N�g�� �ɕ��s�ȃx�N�g�����e�_�ŕ`���B���̂����ł`�A�a�A�b������Ă`�ɖ߂��Ă���B�Ō�ɓ_�`�ŕ`���ꂽ�x�N�g���͋�� �����R�ł��邽�߁A���Ƃ̃x�N�g���ɕ��s�ł���B

���ʏ�ł͏�̏ꍇ�ƑS���قȂ�B�`����o�����ĕ��s�ړ������Ȃ���a�A�b������Ă`�ɖ߂��Ă������̃x�N�g���͍ŏ� �̃x�N�g���ɕ��s�łȂ��B���̗l�Ȑ����͋Ȗʂ̈�ʓI�Ȑ����ŁA���R�ȋ�Ԃł͋N����Ȃ��B�Ȃ�����Ԃł͋Ǐ��I�ɂ� �x�N�g���s�ɕۂ��Ă��̒�����ς��Ȃ��悤�Ɉړ����鎖���o���邪�A���I�ɕ��s�ȃx�N�g������`���鎖�͕s�\�ł���B
��ŏq�ׂ����s�ړ��𐔎��ŕ\���B
�x�N�g����
 �����}�̗l�ɂ���Ȑ���̊e�_�Œ�`����Ă���B
�����}�̗l�ɂ���Ȑ���̊e�_�Œ�`����Ă���B�x�N�g��
 ��
��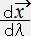 �͋Ȑ��ɐڂ���x�N�g���ł���B�i
�͋Ȑ��ɐڂ���x�N�g���ł���B�i 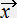 �͋Ȑ��̈ʒu�x�N�g���B�ɂ͋Ȑ��ɉ� �����p�����[�^�[ �j
�͋Ȑ��̈ʒu�x�N�g���B�ɂ͋Ȑ��ɉ� �����p�����[�^�[ �j�@�@�@
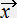 ���i�w0�C�w1�C�w2�C�w 3�j
���i�w0�C�w1�C�w2�C�w 3�j�@�@�@
 ���i
���i  �C
�C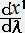 �C
�C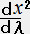 �C
�C �j
�j�@�@�@
 ��
��
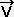 �����s�ړ��̎��A�Ǐ������n�ł͓_�o�ł�
�����s�ړ��̎��A�Ǐ������n�ł͓_�o�ł� 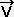 �� �����͋Ȑ��ɉ����Ĉ��łȂ��Ă͂Ȃ�Ȃ��B����
�� �����͋Ȑ��ɉ����Ĉ��łȂ��Ă͂Ȃ�Ȃ��B�����@�@�@
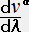 ���O
���O�����������
�@�@�@
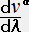 ���t���u���C��=�t ���u���G�����O
���t���u���C��=�t ���u���G�����O�t���u���G�����O�����藧�̂́A�Ǐ������n�ł̓N���X�g�b�t�F���L���i���� ���ʃ��j���O������ł���B
�̂ɕ��s�ړ��̏����Ƃ���
�@�@�@���@�t���u���G�����O�@�@
 �@�@ �u���G�����O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�U�j
�@�@ �u���G�����O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�U�j�u���G�����O �̓e���\���������Ȃ̂ň�ʂ̌n�ł����藧���ł���B

�S. ���@�n�@��
���n���Ƃ͓�̓_�����ԍŒZ�̌o�H�̎��ł���B�Ǐ������n�ł͕��̂͏d�͂������Ȃ��Œ����^��������B���̋O���ɉ����Ď��X�ƋǏ������n���Ȃ��ł����Ε��̂̉^���̋O�Ղ�������B
�O�͂ň�ʂ̃x�N�g�� 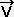 �̕��s�ړ����l�����B����
�̕��s�ړ����l�����B���� 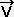 ��
��  �ɑウ���A�����ڐ��x�N�g��
�ɑウ���A�����ڐ��x�N�g��  �s�ړ��������������n���̕������ɂȂ�B
�s�ړ��������������n���̕������ɂȂ�B
�@�@�@�t���t���G�����t���t���C���{�����ʃ� �t���t�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�V�j
�ɂ��Ȑ��̃p�����[�^�[�Ƃ���ƁA�t���t���C��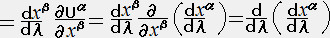 �@�Ȃ̂ŏ�̎���
�@�Ȃ̂ŏ�̎���
�@�@�@���@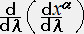 �{�����ʃ�
�{�����ʃ� 
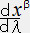 �� �O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�W�j
�� �O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�W�j
�ƂȂ�B���ꂪ���n���̕������ł���B�N���X�g�b�t�F���L���͍��W�o�w���p�̊��m���ł��邩��A���̎��͂w���i�Ɂj�̂S���A���Q�K����`�̔����������ł���B����� �Ɂ���0 �� �w��0���w���i��0�j �� �t��0���i���w���^���Ɂj��0 �Ƃ��������������^�����������̉������B�]���ď����̈ʒu�i�w��0�j�Ə����̕����i�t��0�j��^���鎖�ł�����̑��n����������B
���R�ȋ�Ԃł̓N���X�g�b�t�F���L���͏�����̂ő��n���̎���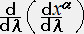 �� �O �ƂȂ�B����������Ɓi���Łj
�� �O �ƂȂ�B����������Ɓi���Łj
�@�@�@X1�����Ɂ{���@�C�@X2�����Ɂ{���@ �@Y=AX +B
�@Y=AX +B
�ƒ����̎��ƂȂ�B
�Ȃ�����Ԃ̎��ɂ́A�d�͏�̕������Ń��g���b�N�����߂鎖�ŃN���X�g�b�t�F���L���̒l�����܂�B����𑪒n���̕������ɑ�����đ��n�������߂�B
�ɂ����鑪�n���̃p�����[�^�[�ŁA�V�����p�����[�^�[��萔���������g����
�@�@�@�������Ɂ{��
�Œ�`��������͏�L�̑��n���̕����������藧�p�����[�^�[�ł�����
�@�@�@ �{ �����ʃ�
�{ �����ʃ� 
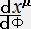 �� �O
�� �O
�ƂȂ�B��ʓI�ɂ����̂悤�ȃɂ̐��`�ϊ��ɂ���Ă̂ݑ��n���̕����������V�����p�����[�^�[���^������B���̂悤�ȃɂ����̂悤�ȃp�����[�^�[���A�t�B���p�����[�^�[�Ƃ����B
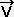 �̕��s�ړ����l�����B����
�̕��s�ړ����l�����B���� 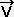 ��
��  �ɑウ���A�����ڐ��x�N�g��
�ɑウ���A�����ڐ��x�N�g��  �s�ړ��������������n���̕������ɂȂ�B
�s�ړ��������������n���̕������ɂȂ�B�@�@�@�t���t���G�����t���t���C���{�����ʃ� �t���t�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�V�j
�ɂ��Ȑ��̃p�����[�^�[�Ƃ���ƁA�t���t���C��
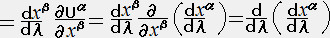 �@�Ȃ̂ŏ�̎���
�@�Ȃ̂ŏ�̎����@�@�@���@
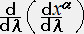 �{�����ʃ�
�{�����ʃ� 
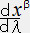 �� �O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�W�j
�� �O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�W�j�ƂȂ�B���ꂪ���n���̕������ł���B�N���X�g�b�t�F���L���͍��W�o�w���p�̊��m���ł��邩��A���̎��͂w���i�Ɂj�̂S���A���Q�K����`�̔����������ł���B����� �Ɂ���0 �� �w��0���w���i��0�j �� �t��0���i���w���^���Ɂj��0 �Ƃ��������������^�����������̉������B�]���ď����̈ʒu�i�w��0�j�Ə����̕����i�t��0�j��^���鎖�ł�����̑��n����������B
���R�ȋ�Ԃł̓N���X�g�b�t�F���L���͏�����̂ő��n���̎���
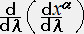 �� �O �ƂȂ�B����������Ɓi���Łj
�� �O �ƂȂ�B����������Ɓi���Łj�@�@�@X1�����Ɂ{���@�C�@X2�����Ɂ{���@
 �@Y=AX +B
�@Y=AX +B�ƒ����̎��ƂȂ�B
�Ȃ�����Ԃ̎��ɂ́A�d�͏�̕������Ń��g���b�N�����߂鎖�ŃN���X�g�b�t�F���L���̒l�����܂�B����𑪒n���̕������ɑ�����đ��n�������߂�B
�ɂ����鑪�n���̃p�����[�^�[�ŁA�V�����p�����[�^�[��萔���������g����
�@�@�@�������Ɂ{��
�Œ�`��������͏�L�̑��n���̕����������藧�p�����[�^�[�ł�����
�@�@�@
 �{ �����ʃ�
�{ �����ʃ� 
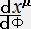 �� �O
�� �O�ƂȂ�B��ʓI�ɂ����̂悤�ȃɂ̐��`�ϊ��ɂ���Ă̂ݑ��n���̕����������V�����p�����[�^�[���^������B���̂悤�ȃɂ����̂悤�ȃp�����[�^�[���A�t�B���p�����[�^�[�Ƃ����B
�T. �ȁ@���@�e�@���@�\�@��
���g���b�N�͎����R�ł��邩�Ȃ��Ă��邩��\���A���̂P�K�����͎���̌X���i���z�j�Ƃ������ׂ��ʂł��邩��A�N���X�g�b�t�F���L���͎���̊e�_�ɂ�����ڐ���ڕ��ʂ̌X���̂悤�ɋ����͈͂̒����I�Ȑ�����\��������̂ł���B�ȗ��e���\���̓��g���b�N�̂Q�K�����ł��邩��A����͐ڕ��ʂ̌X�����ω����銄����\���A�Ȗʂ̋ȗ�������Â�����̂ł���B
�ȗ������߂邽�߂Ɂ@�u�R. ���@�s�@�ځ@���v�@�ŏq�ׂ������Ȑ��̂܂��Ńx�N�g���s�ړ������ɖ߂�B�Ȗʂ̏�Ńx�N�g���s�ړ����鎞�A�o�H�ɂ���Ă����������ʂɂȂ�B�����\���̂����[�}���̋ȗ��e���\���ł���A������ȗ��̒�`�Ɏg���B
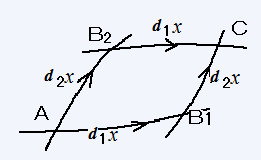
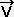 ���_�a1�ɕ��s�ړ������B���s�ړ��̖@
���@�u���G�����u���C���{���������u �����O�@���
���_�a1�ɕ��s�ړ������B���s�ړ��̖@
���@�u���G�����u���C���{���������u �����O�@���
�@�@�@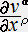 ���[���������u��
���[���������u��
�]���ē_�a1�ł̃x�N�g���̐�����
�@�@�@�u���i�a1�j �� �u���i�`)�{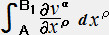 �� �u���i�`)�[
�� �u���i�`)�[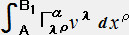
�@�@�@�@�@�@�@�@�@�� �u���i�`)�[���������u���i�`)�� 1�w���@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�X�j
�@�@�@�@�@�@�@�@ ���l�ɓ_�a1����_�b�֕��s�ړ����������̓_�b�ł̃x�N�g���̐�����
�@�@�@�u���i�b�j �� �u���i�a1)�[�m���������n B1 �u���i�a1)��2�w���@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�O�j
�@�@�@�@ �m���������nB1 �͓_�a1�ɉ����� �������� �̒l�ŁA�P�Ȃ� �������� �͓_�`�ɉ��� ��l�ł���B
�@�@�@�m���������nB1 �� ���������{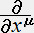 ����������1�w��
����������1�w��
�ł���B�]����
�@�@�@�m���������nB1 �u���i�a1) �� �i���������{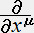 ����������1�w���j�i�u���i�`)�[ ���������u���i�`)��1�w���j
����������1�w���j�i�u���i�`)�[ ���������u���i�`)��1�w���j
�@�@�@ ���������u���i�`)�[ �����������������u���i�`)��1�w��
�{�i
���������u���i�`)�[ �����������������u���i�`)��1�w��
�{�i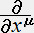 ����������1�w�� �j�i�u���i�`)�j
�@�E�E�E�E�E�@�i�Q�P�j
����������1�w�� �j�i�u���i�`)�j
�@�E�E�E�E�E�@�i�Q�P�j
�i�P�X�j�Ɓi�Q�P�j���i�Q�O�j�̉E�ӂɑ�������
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��1�w��
�@�@�@�@�@�@�[�m���������u���i�`)�[ �����������������u���i�`)��1�w�� �{�i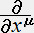 ����������1�w�� �j�i�u���i�`)�j]��2�w��
����������1�w�� �j�i�u���i�`)�j]��2�w��
�@�@�@�� �u���i�`)�[���������u���i�`)��1�w ���[���������u���i�`)��2�w��
�@�@�@�@�@�{�����������������u���i�`)��1�w ����2�w�� �[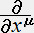 ���������u���i�`)�� 1�w����2�w��
���������u���i�`)�� 1�w����2�w��
��̎��̉E�ӂ̑�l���̃_�~�[�̓Y���A�Ɂ����C�����сC�����ʁ@�ɂ��ꂼ�ꏑ���������
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��1�w���[���������u���i�`)��2�w ��
�@�@�@�@�@�@�@�@�@�{�������������u���i�`)�� 1�w����2�w�� �[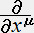 ���������u���i�`)�� 1�w����2�w��
���������u���i�`)�� 1�w����2�w��
�E�ӂ̑�O���Ƒ�l�������ʍ��A�u���i�`)��1�w����2�w���� �����
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��1�w���[���������u���i�`)��2�w ��
�@�@�@�@�@�@�@�@�@�{�i������������ �[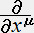 ���������j�u���i�`)�� 1�w����2�w���@
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�Q�j
���������j�u���i�`)�� 1�w����2�w���@
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�Q�j
��̎����`���a1���b�ƃx�N�g���s�ړ����������̂b�_�ɉ�����x�N�g���̐����ł���B
�`���a2���b�ƃx�N�g���s�ړ����������̂b�_�ɉ�����x�N�g���̐��������l�Ɍv�Z���ċ��܂邪�A�i�Q�Q�j �̎�����1�w����2�w����芷����ΊȒP�ɋ��܂�B����
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��2�w���[���������u���i�`)��1�w ��
�@�@�@�@�@�@�@�@�@�{�i������������ �[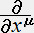 ���������j�u���i�`)�� 2�w����1�w��
���������j�u���i�`)�� 2�w����1�w��
�_�~�[�̓Y�������ꂼ�ꏑ���������
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��2�w���[���������u���i�`)��1�w ��
�@�@�@�@�@�@�@�@�@�{�i������������ �[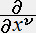 ���������j�u���i�`)�� 1�w����2�w��
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�R�j
���������j�u���i�`)�� 1�w����2�w��
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�R�j
�i�Q�R�j����i�Q�Q�j�������A�o�H�̈Ⴂ�ɂ��_�b�ł̃x�N�g���̐����̍��A�u���i�b�j�����߂��
�@�@�@�u���i�b�j �� �q�����ʃ��u���i�`)�� 1�w����2�w��
������
�@�@�@���@�q�����ʃ� �� �������ˁC���[ �������ʁC���{�����у����������[ �����у��������� �@�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�S�j
�q�����ʃ��́u���[�}���̋ȗ��e���\���v�ƌĂ�A���[�N���b�h�w�̕��s���̌����̔j��A������Ԃ̘c�݂̒��x��\���l�K�́i�P�C�R�j�e���\���ł���B ��Ԃ����R�Ȃ� �q�����ʃ� �� �O �ł���B
�ȗ������߂邽�߂Ɂ@�u�R. ���@�s�@�ځ@���v�@�ŏq�ׂ������Ȑ��̂܂��Ńx�N�g���s�ړ������ɖ߂�B�Ȗʂ̏�Ńx�N�g���s�ړ����鎞�A�o�H�ɂ���Ă����������ʂɂȂ�B�����\���̂����[�}���̋ȗ��e���\���ł���A������ȗ��̒�`�Ɏg���B

���}�̂悤�ɁA��Ԃ̒��ɔ��ɏ����������Ȑ����l����B�Ȗʂɂ����ăx�N�g���u�����`����a1���o�Ăb�܂Ŕ��������������s�ړ����������ƁA�`����a2���o�Ăb�܂ŕ��s�ړ����������Ƃł͈�ʂɂ��������ʂɂȂ�B���̂������͋Ȗʂ̋ȗ��ƊW������B
�_�`�Œ�`���ꂽ�x�N�g�� 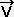 ���_�a1�ɕ��s�ړ������B���s�ړ��̖@
���@�u���G�����u���C���{���������u �����O�@���
���_�a1�ɕ��s�ړ������B���s�ړ��̖@
���@�u���G�����u���C���{���������u �����O�@����@�@�@
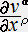 ���[���������u��
���[���������u���]���ē_�a1�ł̃x�N�g���̐�����
�@�@�@�u���i�a1�j �� �u���i�`)�{
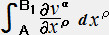 �� �u���i�`)�[
�� �u���i�`)�[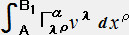
�@�@�@�@�@�@�@�@�@�� �u���i�`)�[���������u���i�`)�� 1�w���@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�X�j
�@�@�@�@�@�@�@�@ ���l�ɓ_�a1����_�b�֕��s�ړ����������̓_�b�ł̃x�N�g���̐�����
�@�@�@�u���i�b�j �� �u���i�a1)�[�m���������n B1 �u���i�a1)��2�w���@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�O�j
�@�@�@�@ �m���������nB1 �͓_�a1�ɉ����� �������� �̒l�ŁA�P�Ȃ� �������� �͓_�`�ɉ��� ��l�ł���B
�@�@�@�m���������nB1 �� ���������{
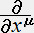 ����������1�w��
����������1�w��
�ł���B�]����
�@�@�@�m���������nB1 �u���i�a1) �� �i���������{
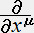 ����������1�w���j�i�u���i�`)�[ ���������u���i�`)��1�w���j
����������1�w���j�i�u���i�`)�[ ���������u���i�`)��1�w���j�@�@�@
 ���������u���i�`)�[ �����������������u���i�`)��1�w��
�{�i
���������u���i�`)�[ �����������������u���i�`)��1�w��
�{�i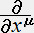 ����������1�w�� �j�i�u���i�`)�j
�@�E�E�E�E�E�@�i�Q�P�j
����������1�w�� �j�i�u���i�`)�j
�@�E�E�E�E�E�@�i�Q�P�j�i�P�X�j�Ɓi�Q�P�j���i�Q�O�j�̉E�ӂɑ�������
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��1�w��
�@�@�@�@�@�@�[�m���������u���i�`)�[ �����������������u���i�`)��1�w�� �{�i
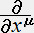 ����������1�w�� �j�i�u���i�`)�j]��2�w��
����������1�w�� �j�i�u���i�`)�j]��2�w���@�@�@�� �u���i�`)�[���������u���i�`)��1�w ���[���������u���i�`)��2�w��
�@�@�@�@�@�{�����������������u���i�`)��1�w ����2�w�� �[
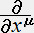 ���������u���i�`)�� 1�w����2�w��
���������u���i�`)�� 1�w����2�w�� ��̎��̉E�ӂ̑�l���̃_�~�[�̓Y���A�Ɂ����C�����сC�����ʁ@�ɂ��ꂼ�ꏑ���������
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��1�w���[���������u���i�`)��2�w ��
�@�@�@�@�@�@�@�@�@�{�������������u���i�`)�� 1�w����2�w�� �[
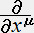 ���������u���i�`)�� 1�w����2�w��
���������u���i�`)�� 1�w����2�w�� �E�ӂ̑�O���Ƒ�l�������ʍ��A�u���i�`)��1�w����2�w���� �����
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��1�w���[���������u���i�`)��2�w ��
�@�@�@�@�@�@�@�@�@�{�i������������ �[
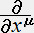 ���������j�u���i�`)�� 1�w����2�w���@
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�Q�j
���������j�u���i�`)�� 1�w����2�w���@
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�Q�j��̎����`���a1���b�ƃx�N�g���s�ړ����������̂b�_�ɉ�����x�N�g���̐����ł���B
�`���a2���b�ƃx�N�g���s�ړ����������̂b�_�ɉ�����x�N�g���̐��������l�Ɍv�Z���ċ��܂邪�A�i�Q�Q�j �̎�����1�w����2�w����芷����ΊȒP�ɋ��܂�B����
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��2�w���[���������u���i�`)��1�w ��
�@�@�@�@�@�@�@�@�@�{�i������������ �[
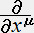 ���������j�u���i�`)�� 2�w����1�w��
���������j�u���i�`)�� 2�w����1�w�� �_�~�[�̓Y�������ꂼ�ꏑ���������
�@�@�@�u���i�b�j �� �u���i�`)�[���������u���i �`)��2�w���[���������u���i�`)��1�w ��
�@�@�@�@�@�@�@�@�@�{�i������������ �[
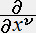 ���������j�u���i�`)�� 1�w����2�w��
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�R�j
���������j�u���i�`)�� 1�w����2�w��
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�R�j�i�Q�R�j����i�Q�Q�j�������A�o�H�̈Ⴂ�ɂ��_�b�ł̃x�N�g���̐����̍��A�u���i�b�j�����߂��
�@�@�@�u���i�b�j �� �q�����ʃ��u���i�`)�� 1�w����2�w��
������
�@�@�@���@�q�����ʃ� �� �������ˁC���[ �������ʁC���{�����у����������[ �����у��������� �@�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�S�j
�q�����ʃ��́u���[�}���̋ȗ��e���\���v�ƌĂ�A���[�N���b�h�w�̕��s���̌����̔j��A������Ԃ̘c�݂̒��x��\���l�K�́i�P�C�R�j�e���\���ł���B ��Ԃ����R�Ȃ� �q�����ʃ� �� �O �ł���B
�U. ���n�����̕�����
�Ȃ��������W�n�ł͕��s���͉������Ă����ƕ��s�łȂ��Ȃ�B���̎������[�}���e���\���y�јA���x�N�g�����g���Ē莮�����������������n�����̕������Ƃ����B

�@�@�@ ���O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�T�j
���O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�T�j
�ƂȂ�B�_�`'�ł̓N���X�g�b�t�F���L���͏����Ȃ��̂ŁA�_�`'�ł̑��n����������
�@�@�@ �{����00�i�`'�j���O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�U�j
�{����00�i�`'�j���O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�U�j
�ł���B�����œ_�`'�ɉ����Ă�͂�u��������0�ƂȂ�悤�ɍ��W�n��I�B �`�Ƃ`'�� ������������Ă��Ȃ��̂�
������������Ă��Ȃ��̂�
�@�@�@����00�i�`'�j ����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�V�j
����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�V�j
�����藧�B�i�e�[���[�̒藝 f�ia�{x�j�|f�ia�j xf'�ia�j �����p����B�j
xf'�ia�j �����p����B�j
���i�Q�U�j�Ɓi�Q�V�j���
�@�@�@ ���[����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�W�j
�x�N�g��
���[����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�W�j
�x�N�g��  �̐��������́A�����i�ɁC���n��
�̐��������́A�����i�ɁC���n�� �j�[�����i�ɁC���n��
�j�[�����i�ɁC���n�� �j�ŗ^������B�]���ē_�`��
�j�ŗ^������B�]���ē_�`��
�@�@�@ ��
��  �[
�[  �� �[����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�X�j
�ƂȂ�B���������̊��S�ȂQ�K�̋��ϔ����A��v��v
�� �[����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�X�j
�ƂȂ�B���������̊��S�ȂQ�K�̋��ϔ����A��v��v �����߂�B
�����߂�B
�@�@�@��v��v���� �� ��v�i��v�����j �� �i��v�����j�{������0�i��v�����j
�@�E�E�E�E�E�E�E�E�E�@�i�R�O�j
�i��v�����j�{������0�i��v�����j
�@�E�E�E�E�E�E�E�E�E�@�i�R�O�j
�@�@�@�@�@�@�i�Ō�̍��̃N���X�g�b�t�F���L���̓Y��0�� ���Ɂ����с����� ���0�ł���j
�Ǐ������n�ł͓_�`�ɂ����ăN���X�g�b�t�F���L���͏����i������0���O�j�A�N���X�g�b�t�F���L���̔����͏����Ȃ��̂�
�@�@�@��v��v���� �� �i��v�����j ��
�i��v�����j ��  �i
�i �����{������0�����j ��
�����{������0�����j ��  �����{������0,0����
�����{������0,0����
���_�`�Ő��藧�B���i�Q�X�j�Ə�̎����
�@�@�@��v��v���� �� �i������0,0�[����00,���j���� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�P�j
���i�Q�S�j���A������0,0�[����00,�� �� �q��00���Ȃ̂�
�@�@�@��v��v���� �� �q��00������ �� �q���ʃ˃��u���u�������@�@�i�� �u���� ����0������j
��������B�ŏI�I�Ȍ��ʂ͌n�Ɉˑ������A�]���āA�C�ӂ�����
�@�@�@���@��v��v���� �� �q���ʃ˃��u���u�������@�@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�Q�j
�ł���B���R�ȋ�Ԃł̑��n���� �q���ʃ˃����O �Ȃ̂ł��̊Ԋu�͕ω����Ȃ��B�������A�Ȃ�������Ԃł͂��̊Ԋu�͕ω�����B���̎������n�����̕������Ƃ����B���̎����d�͔g�̕����v�Z���鎞�ɗp������B

���}�̗l�ɓ_�`�Ƃ`'�ɉ����ĕ��s�Ō݂��ɐڋ߂����ڃx�N�g��  ��
��  �����A��̑��n�����l����B�A�t�B���p�����[�^�[���ɂƂ���B�i�ɂ͋Ȑ��ɉ������p�����[�^������сi���ŗL���ԁj�ł��悢�j
�����A��̑��n�����l����B�A�t�B���p�����[�^�[���ɂƂ���B�i�ɂ͋Ȑ��ɉ������p�����[�^������сi���ŗL���ԁj�ł��悢�j
������瑼���֒B�����A���x�N�g�� ���`����B����
���`����B����  �̓ɂő����ē����Ԋu�̓_�ǂ�����A��������̂ł���B
(�Ⴆ�`�Ƃ`'�A�a�Ƃa'�̂悤��)
�̓ɂő����ē����Ԋu�̓_�ǂ�����A��������̂ł���B
(�Ⴆ�`�Ƃ`'�A�a�Ƃa'�̂悤��)
�ȒP���̂��߂ɓ_�`�ł̋Ǐ������n���W���Ƃ�A���̒��ō��W���w0�Ƒ��n���̕�������v���Ă���Ƃ���B�]���ē_�`�ł͂u��������0�ł���B
�_�`�ł͑S�ẴN���X�g�b�t�F���L���������邩��A�_�`�ł̑��n���������� ��
��  �����A��̑��n�����l����B�A�t�B���p�����[�^�[���ɂƂ���B�i�ɂ͋Ȑ��ɉ������p�����[�^������сi���ŗL���ԁj�ł��悢�j
�����A��̑��n�����l����B�A�t�B���p�����[�^�[���ɂƂ���B�i�ɂ͋Ȑ��ɉ������p�����[�^������сi���ŗL���ԁj�ł��悢�j������瑼���֒B�����A���x�N�g��
 ���`����B����
���`����B����  �̓ɂő����ē����Ԋu�̓_�ǂ�����A��������̂ł���B
(�Ⴆ�`�Ƃ`'�A�a�Ƃa'�̂悤��)
�̓ɂő����ē����Ԋu�̓_�ǂ�����A��������̂ł���B
(�Ⴆ�`�Ƃ`'�A�a�Ƃa'�̂悤��)�ȒP���̂��߂ɓ_�`�ł̋Ǐ������n���W���Ƃ�A���̒��ō��W���w0�Ƒ��n���̕�������v���Ă���Ƃ���B�]���ē_�`�ł͂u��������0�ł���B
�@�@�@
 ���O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�T�j
���O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�T�j�ƂȂ�B�_�`'�ł̓N���X�g�b�t�F���L���͏����Ȃ��̂ŁA�_�`'�ł̑��n����������
�@�@�@
 �{����00�i�`'�j���O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�U�j
�{����00�i�`'�j���O
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�U�j�ł���B�����œ_�`'�ɉ����Ă�͂�u��������0�ƂȂ�悤�ɍ��W�n��I�B �`�Ƃ`'��
 ������������Ă��Ȃ��̂�
������������Ă��Ȃ��̂��@�@�@����00�i�`'�j
 ����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�V�j
����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�V�j�����藧�B�i�e�[���[�̒藝 f�ia�{x�j�|f�ia�j
 xf'�ia�j �����p����B�j
xf'�ia�j �����p����B�j���i�Q�U�j�Ɓi�Q�V�j���
�@�@�@
 ���[����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�W�j
�x�N�g��
���[����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�W�j
�x�N�g��  �̐��������́A�����i�ɁC���n��
�̐��������́A�����i�ɁC���n�� �j�[�����i�ɁC���n��
�j�[�����i�ɁC���n�� �j�ŗ^������B�]���ē_�`��
�j�ŗ^������B�]���ē_�`���@�@�@
 ��
��  �[
�[  �� �[����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�X�j
�ƂȂ�B���������̊��S�ȂQ�K�̋��ϔ����A��v��v
�� �[����00,������
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�X�j
�ƂȂ�B���������̊��S�ȂQ�K�̋��ϔ����A��v��v �����߂�B
�����߂�B�@�@�@��v��v���� �� ��v�i��v�����j ��
 �i��v�����j�{������0�i��v�����j
�@�E�E�E�E�E�E�E�E�E�@�i�R�O�j
�i��v�����j�{������0�i��v�����j
�@�E�E�E�E�E�E�E�E�E�@�i�R�O�j�@�@�@�@�@�@�i�Ō�̍��̃N���X�g�b�t�F���L���̓Y��0�� ���Ɂ����с����� ���0�ł���j
�Ǐ������n�ł͓_�`�ɂ����ăN���X�g�b�t�F���L���͏����i������0���O�j�A�N���X�g�b�t�F���L���̔����͏����Ȃ��̂�
�@�@�@��v��v���� ��
 �i��v�����j ��
�i��v�����j ��  �i
�i �����{������0�����j ��
�����{������0�����j ��  �����{������0,0����
�����{������0,0�������_�`�Ő��藧�B���i�Q�X�j�Ə�̎����
�@�@�@��v��v���� �� �i������0,0�[����00,���j���� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�P�j
���i�Q�S�j���A������0,0�[����00,�� �� �q��00���Ȃ̂�
�@�@�@��v��v���� �� �q��00������ �� �q���ʃ˃��u���u�������@�@�i�� �u���� ����0������j
��������B�ŏI�I�Ȍ��ʂ͌n�Ɉˑ������A�]���āA�C�ӂ�����
�@�@�@���@��v��v���� �� �q���ʃ˃��u���u�������@�@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�Q�j
�ł���B���R�ȋ�Ԃł̑��n���� �q���ʃ˃����O �Ȃ̂ł��̊Ԋu�͕ω����Ȃ��B�������A�Ȃ�������Ԃł͂��̊Ԋu�͕ω�����B���̎������n�����̕������Ƃ����B���̎����d�͔g�̕����v�Z���鎞�ɗp������B
�V. �r�A���L�̍P����
�r�A���L�̍P�������ؖ�����O�ɓ_�o�ɉ�����Ǐ������n�ł�
���[�}���̋ȗ��e���\���q�̐����ׂĂ����B
�Ǐ������n�ł� �����ʃ����O �ł��邪�A���g���b�N�̂Q�K�̔����͂O�łȂ�����
�@�@�@�����ʃˁC���� ������ �i ������,�˃��{������,�ʃ��[���ʃ�,���� �j
������ �i ������,�˃��{������,�ʃ��[���ʃ�,���� �j
�_�o�� �����ʃ����O ������A���i�Q�S�j�̃��[�}���̋ȗ��̉E�ӂ̑�O���i�����у����������j��
��l���i �����у����������j�͂O�ƂȂ�B�]����
�@�@�@�q�����ʃ� �� �������ˁC���[ �������ʁC�� �� ������ �i ���Ѓ�,�˃��{���Ѓ�,�����[������,�Ѓ�
������ �i ���Ѓ�,�˃��{���Ѓ�,�����[������,�Ѓ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�[���Ѓ�,�ʃ��[���Ѓ�,�����{������,�Ѓ��j
���g���b�N�͑Ώ̂ŁA�Δ����͏�Ɍ����\������ ���Ѓ�,�˃������Ѓ�,�ʃ�
����āA�_�o�ɉ�����Ǐ������n�ł� ���[�}���̋ȗ��e���\���q��
�@�@�@���@�q�����ʃ� �� ������ �i���Ѓ�,�����[���Ѓ�,�����{������, �Ѓ��[������,�Ѓ��j
�@�@�E�E�E�E�E�E�E�E�E�E�E�@�i�R�R�j
��������B�Y�������i�_�o�ł̂��̍��W�n�Łj�������
������ �i���Ѓ�,�����[���Ѓ�,�����{������, �Ѓ��[������,�Ѓ��j
�@�@�E�E�E�E�E�E�E�E�E�E�E�@�i�R�R�j
��������B�Y�������i�_�o�ł̂��̍��W�n�Łj�������
�@�@�@�q�����ʃ� �� �������q�����ʃ� �� ���������Ƀ� �i ���Ѓ�,�����[���Ѓ�,�����{������,�Ѓ��[������,�Ѓ��j
���������Ƀ� �i ���Ѓ�,�����[���Ѓ�,�����{������,�Ѓ��[������,�Ѓ��j
���������Ƀ��� �����Ɂ��Ђ̎������O�łȂ�����
�@�@�@���@�q�����ʃ� �� �i������, �����[������,�����{������,�����[������,���� �j
�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�S�j
�i������, �����[������,�����{������,�����[������,���� �j
�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�S�j
��̎���艺�L�̓�̎����e�Ղɓ������B
�@�@�@���@�q�����ʃ����[�q�����ʃ����|�q�����˃����q�ʃ˃����E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�T�j
�@�@�@���@�q�����ʃ��{�q���˃����{�q���ʃ˃����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�U�j
���i�R�T�j�ɉ����āA�q�����ʃ��͍ŏ��̓�̓Y���̒��ł̓��ꊷ���ɂ��ĂƁA�����̓�̓Y���̒��ł� ���ꊷ���ɂ��Ĕ��Ώ̂ł���A�ŏ��̓�̓Y���Ǝ��̓�̓Y���̓����̓��ꊷ���ɑ��đΏ̂ł���B
���ׁ̈A�q�����ʃ��̓Ɨ��Ȑ����̐����Q�P���ɂȂ�B
���i�R�U�j�͎��i�R�T�j�ƓƗ��ȓƗ��Ȃ��̂Ƃ��ẮA������̊W����^���A�]���ēƗ��Ȑ����̐����Q�O�Ɍ��炷�B
�i�R�R�j�Ɓi�R�S�j�͋��ϔ����łȂ��Δ��������邩��e���\���������łȂ��B�]���Ă��̌`�������ꂽ���W�n�݂̂Ő��藧���ł���B�i�R�T�j�Ɓi�R�U�j�͈�̍��W�n�Ő��藧�e���\��������������A�S�Ă̊��ɑ��Đ��藧�B
�i�R�S�j�������Ŕ������A���̌��ʂ��Ǐ������n�ōl����B
�@�@�@�q�����ʃ�,�� �� �i������, ���ʃ��[������,���˃��{������,���˃��[������,���� �� �j
�i������, ���ʃ��[������,���˃��{������,���˃��[������,���� �� �j
��̎��ɂ����ēY���i��,��,�ˁj�����ɓ���ւ������A�q�����ʃ�,���@�A�q�����Ƀ�,���@�A�q �����˃�,�������ꂼ�������ƁA�Δ����͌����\�i���Δ������鏇���̖��W���j������O�ɂȂ�B
�@�@�@�q�����ʃ�,���{�q�����Ƀ�,���{�q�����˃�,�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�V�j
�Ǐ������n�ł� �����������O �����牺�L�̎������藧�B
�@�@�@���@�q�����ʃˁG���{�q�����ɃʁG���{�q�����˃ɁG�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�W�j
���̎��̓e���\���������Ȃ̂ŁA�C�ӂ̌n�Ő��藧�B������u�r�A���L�̍P�����v�Ƃ����B�Y��������t���ɂ������L�̎������藧�B
�@�@�@���@�q�����ʃˁG���{�q�����ɃʁG���{�q�����˃ɁG�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�X�j
�y�ؖ��z
�Ǐ������n�ł� �����ʃ����O �ł��邪�A���g���b�N�̂Q�K�̔����͂O�łȂ�����
�@�@�@�����ʃˁC����
 ������ �i ������,�˃��{������,�ʃ��[���ʃ�,���� �j
������ �i ������,�˃��{������,�ʃ��[���ʃ�,���� �j�_�o�� �����ʃ����O ������A���i�Q�S�j�̃��[�}���̋ȗ��̉E�ӂ̑�O���i�����у����������j��
��l���i �����у����������j�͂O�ƂȂ�B�]����
�@�@�@�q�����ʃ� �� �������ˁC���[ �������ʁC�� ��
 ������ �i ���Ѓ�,�˃��{���Ѓ�,�����[������,�Ѓ�
������ �i ���Ѓ�,�˃��{���Ѓ�,�����[������,�Ѓ��@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�[���Ѓ�,�ʃ��[���Ѓ�,�����{������,�Ѓ��j
���g���b�N�͑Ώ̂ŁA�Δ����͏�Ɍ����\������ ���Ѓ�,�˃������Ѓ�,�ʃ�
����āA�_�o�ɉ�����Ǐ������n�ł� ���[�}���̋ȗ��e���\���q��
�@�@�@���@�q�����ʃ� ��
 ������ �i���Ѓ�,�����[���Ѓ�,�����{������, �Ѓ��[������,�Ѓ��j
�@�@�E�E�E�E�E�E�E�E�E�E�E�@�i�R�R�j
��������B�Y�������i�_�o�ł̂��̍��W�n�Łj�������
������ �i���Ѓ�,�����[���Ѓ�,�����{������, �Ѓ��[������,�Ѓ��j
�@�@�E�E�E�E�E�E�E�E�E�E�E�@�i�R�R�j
��������B�Y�������i�_�o�ł̂��̍��W�n�Łj��������@�@�@�q�����ʃ� �� �������q�����ʃ� ��
 ���������Ƀ� �i ���Ѓ�,�����[���Ѓ�,�����{������,�Ѓ��[������,�Ѓ��j
���������Ƀ� �i ���Ѓ�,�����[���Ѓ�,�����{������,�Ѓ��[������,�Ѓ��j���������Ƀ��� �����Ɂ��Ђ̎������O�łȂ�����
�@�@�@���@�q�����ʃ� ��
 �i������, �����[������,�����{������,�����[������,���� �j
�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�S�j
�i������, �����[������,�����{������,�����[������,���� �j
�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�S�j��̎���艺�L�̓�̎����e�Ղɓ������B
�@�@�@���@�q�����ʃ����[�q�����ʃ����|�q�����˃����q�ʃ˃����E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�T�j
�@�@�@���@�q�����ʃ��{�q���˃����{�q���ʃ˃����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�U�j
���i�R�T�j�ɉ����āA�q�����ʃ��͍ŏ��̓�̓Y���̒��ł̓��ꊷ���ɂ��ĂƁA�����̓�̓Y���̒��ł� ���ꊷ���ɂ��Ĕ��Ώ̂ł���A�ŏ��̓�̓Y���Ǝ��̓�̓Y���̓����̓��ꊷ���ɑ��đΏ̂ł���B
���ׁ̈A�q�����ʃ��̓Ɨ��Ȑ����̐����Q�P���ɂȂ�B
���i�R�U�j�͎��i�R�T�j�ƓƗ��ȓƗ��Ȃ��̂Ƃ��ẮA������̊W����^���A�]���ēƗ��Ȑ����̐����Q�O�Ɍ��炷�B
�i�R�R�j�Ɓi�R�S�j�͋��ϔ����łȂ��Δ��������邩��e���\���������łȂ��B�]���Ă��̌`�������ꂽ���W�n�݂̂Ő��藧���ł���B�i�R�T�j�Ɓi�R�U�j�͈�̍��W�n�Ő��藧�e���\��������������A�S�Ă̊��ɑ��Đ��藧�B
�i�R�S�j�������Ŕ������A���̌��ʂ��Ǐ������n�ōl����B
�@�@�@�q�����ʃ�,�� ��
 �i������, ���ʃ��[������,���˃��{������,���˃��[������,���� �� �j
�i������, ���ʃ��[������,���˃��{������,���˃��[������,���� �� �j��̎��ɂ����ēY���i��,��,�ˁj�����ɓ���ւ������A�q�����ʃ�,���@�A�q�����Ƀ�,���@�A�q �����˃�,�������ꂼ�������ƁA�Δ����͌����\�i���Δ������鏇���̖��W���j������O�ɂȂ�B
�@�@�@�q�����ʃ�,���{�q�����Ƀ�,���{�q�����˃�,�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�V�j
�Ǐ������n�ł� �����������O �����牺�L�̎������藧�B
�@�@�@���@�q�����ʃˁG���{�q�����ɃʁG���{�q�����˃ɁG�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�W�j
���̎��̓e���\���������Ȃ̂ŁA�C�ӂ̌n�Ő��藧�B������u�r�A���L�̍P�����v�Ƃ����B�Y��������t���ɂ������L�̎������藧�B
�@�@�@���@�q�����ʃˁG���{�q�����ɃʁG���{�q�����˃ɁG�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�X�j
�y�ؖ��z
�Ǐ������n�ł̓��[�}���̋ȗ��e���\���͉��L�̎��ɂȂ�B
�@�@�@�q�����ʃ� �� �������ˁC���[ �������ʁC���@�@�@�@�@
�ɂŔ�������B�Ǐ������n������
�@�@�@�q�����ʃˁC�� �� �q�����ʃˁG�� �� �������ˁC�ʃ��[ �������ʁC�˃�
�����藧�B ��̎��ɂ����ēY���i��,��,�ˁj�����ɓ���ւ������A�q�����ʃˁG���@�A�q�� ���ɃʁG���@�A�q�� ���˃ɁG�������ꂼ�������ƁA�Δ������鏇���̖��W������O�� �Ȃ�B�]���ēY��������t���̏ꍇ���r�A���L�̍P�����������藧�B���̎��̓e���\���������Ȃ̂ŁA�C�ӂ̌n�Ő��藧 �B
�@�@�@�q�����ʃ� �� �������ˁC���[ �������ʁC���@�@�@�@�@
�ɂŔ�������B�Ǐ������n������
�@�@�@�q�����ʃˁC�� �� �q�����ʃˁG�� �� �������ˁC�ʃ��[ �������ʁC�˃�
�����藧�B ��̎��ɂ����ēY���i��,��,�ˁj�����ɓ���ւ������A�q�����ʃˁG���@�A�q�� ���ɃʁG���@�A�q�� ���˃ɁG�������ꂼ�������ƁA�Δ������鏇���̖��W������O�� �Ȃ�B�]���ēY��������t���̏ꍇ���r�A���L�̍P�����������藧�B���̎��̓e���\���������Ȃ̂ŁA�C�ӂ̌n�Ő��藧 �B
�W. ���b�`�e���\���A���b�`�X�J���[
���[�}���̋ȗ��e���\���ő��Ƒ�O�̓Y�������k�ē�����e���\�������b�`�e���\���Ƃ����B���b�`�e���\�����Ώ̃e���\���ł���B
�@�@�@���@�q�������q�����ʃ����q�����@�@�i�@�q������ �q0��0���{�q1��1���{�q2��2���{�q 3��3���@�j �@�E�E�E�E�E�@�i�S�O�j
���L�̎��ŁA�N���X�g�b�t�F���L�����璼�ڃ��b�`�e���\�������߂鎖���o����B
�@�@�@���@�q�������q�����ʃ�����������,���[ ��������,���{�����Ѓ����������[ �����Ѓ��������� �@�@�E�E�E�E�E�@�i�S�P�j
�y���b�`�e���\���̑Ώ̐��̏ؖ��z
�@�@�@���@�q�����ʃ��q�ʃ������ʃ��������q���ʃ������q���� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�Q�j �@�@�@�@�@�@�@�@�@�@�@�i�q�������������q�����j �@�@
�@�@�@���@�q�������q�����ʃ����q�����@�@�i�@�q������ �q0��0���{�q1��1���{�q2��2���{�q 3��3���@�j �@�E�E�E�E�E�@�i�S�O�j
���L�̎��ŁA�N���X�g�b�t�F���L�����璼�ڃ��b�`�e���\�������߂鎖���o����B
�@�@�@���@�q�������q�����ʃ�����������,���[ ��������,���{�����Ѓ����������[ �����Ѓ��������� �@�@�E�E�E�E�E�@�i�S�P�j
�y���b�`�e���\���̑Ώ̐��̏ؖ��z
�U. �r�A���L�̍P�����̎��i�R�j�ɂ����āA�q�����ʃ����q�ʃ˃��� �̗��ӂ� ������ ���|����B
�@�@�@�������q�����ʃ����������q�ʃ˃����@ �@�q�����ʃ����q���˃���
�@
�@�q�����ʃ����q���˃���
�@ �@�q�������q�˃�
�@�q�������q�˃�
�Y�����@�������@�C�ˁ����@�ɂ��ꂼ�ꏑ��������� �q�������q����
�@�@�@���@���b�`�e���\���͑Ώ̃e���\���ł���B
���l�Ƀ��b�`�e���\�������g���b�N�ŏk�����L�̗ʂ����b�`�X�J���[�����X�J���[�ȗ��Ƃ����B����̓X�J���[�Ȃ̂ŁA���W�̑I�ѕ��ɂ͊W�̂Ȃ��A���̋�Ԃ̋Ȃ�����\���ʂł���B�Ȗʘ_�ŁA�K�E�X�̋ȗ��ƌĂ��ʂ�����B������j�Ƃ���ƁA���b�`�X�J���[�Ƃ̊Ԃ� �q���Q�j �Ƃ����W������B�@�@�@�������q�����ʃ����������q�ʃ˃����@
 �@�q�����ʃ����q���˃���
�@
�@�q�����ʃ����q���˃���
�@ �@�q�������q�˃�
�@�q�������q�˃��Y�����@�������@�C�ˁ����@�ɂ��ꂼ�ꏑ��������� �q�������q����
�@�@�@���@���b�`�e���\���͑Ώ̃e���\���ł���B
�@�@�@���@�q�����ʃ��q�ʃ������ʃ��������q���ʃ������q���� �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�Q�j �@�@�@�@�@�@�@�@�@�@�@�i�q�������������q�����j �@�@
�X. �A�C���V���^�C���E�e���\��
�A�C���V���^�C���E�e���\�����O���������G�����O�A�������G�����O�ł��鎖���m�F���Ă����B�������G�����O���Ȑ����W�n�@�X. �N���X�g�b�t�F���L���ƃ��g���b�N���Q��
�������G���ɂ��Ă͋Ǐ������n�ōl����B�������C�����O������A�������̗v�f����Ȃ�t�s���������̔������O�ł���B����
�@�@�@�������C�����O�@�@�@ �@�@�@�������G�����O�@�@�@�@�i�@��@�Ǐ������n������@�j
�@�@�@�������G�����O�@�@�@�@�i�@��@�Ǐ������n������@�j
����̓e���\���������������ʂ̍��W�n�ł����藧�B ���̓�̎��Ń��g���b�N�͋��ϔ����Ɏ��R�ɏo�����ꂪ�o����B
�r�A���L�̍P�����ɍ��������������|���A���b�`�̏k����{���B
�@�@�@�������m�q�����ʃˁG���{�q�����ɃʁG���{�q�����˃ɁG���n���O
���ϔ����͒ʏ�̔����̐ς̋K���ɏ]������
�@�@�@�i�������q�����ʃ��j�G�����������G���q�����ʃ��{�������q�����ʃˁG�� �@ �@�������q�����ʃˁG�����i�������q�����ʃ��j�G��
�@�������q�����ʃˁG�����i�������q�����ʃ��j�G��
�@�@�@�@�@�@�@�i���b�`�̏k����{������A���ϔ����̋L���@�G���@��t�������Ă��悢�j
�]���đO�q�̎��̑�ꍀ�͂q���ˁG���A��� �ɂƃʂ����Ώ̂�����q�����ɃʁG�����|�q�����ʃɁG���i�U. �r�A���L�̍P�����@ �i�R�j���Q�Ɓj
�]���đ�́|�q���ɁG���A��O���͂q�����˃ɁG��
����ăr�A���L�̍P�����ɍ��������������|�������ʂ�
�@�@�@�q���ˁG���|�q���ɁG���{�q�����˃ɁG�����O�@ �@�q���ˁG���|�q���ɁG���|�q�����ɃˁG�����O
�@�q���ˁG���|�q���ɁG���|�q�����ɃˁG�����O
��̎��ɂ�������������|�����
�@�@�@�q�G���|�q���ɁG���|�q���ɁG�����O�@ �@�q���ɁG���|
�@�q���ɁG���| �q�G�����O
�q�G�����O
�q�G����(�������q�j�G���@������A��̎���
�@�@�@�i�q�����| �������q�j�G�ʁ��O
�������q�j�G�ʁ��O
�ƂȂ�B���Ƀ����|�����
�@�@�@�i�q�ʃ��| ���ʃ��q�j�G�ʁ��O
���ʃ��q�j�G�ʁ��O
�f�ʃ����q�ʃ��| ���ʃ��q�@�Ƃ�����
���ʃ��q�@�Ƃ�����
�@�@�@���@�f�ʃ��G�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�R�j
�@�@�@���@�f�ʃ����q�ʃ��| ���ʃ��q���f�˃�
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�S�j
���ʃ��q���f�˃�
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�S�j
���̑Ώ̂ȃe���\���i���f�ʃ��j���u�A�C���V���^�C���E�e���\���v�Ƃ��� �B���̔��U�i���f�ʃ��G���j�̓[���ł���B�A�C���V���^�C���E�e���\���͏d�͏�̕������̒���
�@�@�@�f�ʃ����W�s�ʃ�
�Ƃ����`�œo�ꂷ��B�s�ʃ��̓X�g���X-�G�l���M�[�e���\���ł���B
�������G���ɂ��Ă͋Ǐ������n�ōl����B�������C�����O������A�������̗v�f����Ȃ�t�s���������̔������O�ł���B����
�@�@�@�������C�����O�@�@�@
 �@�@�@�������G�����O�@�@�@�@�i�@��@�Ǐ������n������@�j
�@�@�@�������G�����O�@�@�@�@�i�@��@�Ǐ������n������@�j����̓e���\���������������ʂ̍��W�n�ł����藧�B ���̓�̎��Ń��g���b�N�͋��ϔ����Ɏ��R�ɏo�����ꂪ�o����B
�r�A���L�̍P�����ɍ��������������|���A���b�`�̏k����{���B
�@�@�@�������m�q�����ʃˁG���{�q�����ɃʁG���{�q�����˃ɁG���n���O
���ϔ����͒ʏ�̔����̐ς̋K���ɏ]������
�@�@�@�i�������q�����ʃ��j�G�����������G���q�����ʃ��{�������q�����ʃˁG�� �@
 �@�������q�����ʃˁG�����i�������q�����ʃ��j�G��
�@�������q�����ʃˁG�����i�������q�����ʃ��j�G���@�@�@�@�@�@�@�i���b�`�̏k����{������A���ϔ����̋L���@�G���@��t�������Ă��悢�j
�]���đO�q�̎��̑�ꍀ�͂q���ˁG���A��� �ɂƃʂ����Ώ̂�����q�����ɃʁG�����|�q�����ʃɁG���i�U. �r�A���L�̍P�����@ �i�R�j���Q�Ɓj
�]���đ�́|�q���ɁG���A��O���͂q�����˃ɁG��
����ăr�A���L�̍P�����ɍ��������������|�������ʂ�
�@�@�@�q���ˁG���|�q���ɁG���{�q�����˃ɁG�����O�@
 �@�q���ˁG���|�q���ɁG���|�q�����ɃˁG�����O
�@�q���ˁG���|�q���ɁG���|�q�����ɃˁG�����O��̎��ɂ�������������|�����
�@�@�@�q�G���|�q���ɁG���|�q���ɁG�����O�@
 �@�q���ɁG���|
�@�q���ɁG���| �q�G�����O
�q�G�����O�q�G����(�������q�j�G���@������A��̎���
�@�@�@�i�q�����|
 �������q�j�G�ʁ��O
�������q�j�G�ʁ��O�ƂȂ�B���Ƀ����|�����
�@�@�@�i�q�ʃ��|
 ���ʃ��q�j�G�ʁ��O
���ʃ��q�j�G�ʁ��O�f�ʃ����q�ʃ��|
 ���ʃ��q�@�Ƃ�����
���ʃ��q�@�Ƃ������@�@�@���@�f�ʃ��G�����O �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�R�j
�@�@�@���@�f�ʃ����q�ʃ��|
 ���ʃ��q���f�˃�
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�S�j
���ʃ��q���f�˃�
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�S�j���̑Ώ̂ȃe���\���i���f�ʃ��j���u�A�C���V���^�C���E�e���\���v�Ƃ��� �B���̔��U�i���f�ʃ��G���j�̓[���ł���B�A�C���V���^�C���E�e���\���͏d�͏�̕������̒���
�@�@�@�f�ʃ����W�s�ʃ�
�Ƃ����`�œo�ꂷ��B�s�ʃ��̓X�g���X-�G�l���M�[�e���\���ł���B
�t�^�P�F�����s��̑Ίp�s��ւ̕ϊ�
�Ώ̂Ȑ����s��`��Ίp�s��i���Ίp�v�f�ȊO�̗v�f�͂O�̍s��j�ɕϊ����A���̑Ίp�v�f��-�P�C�O�C�P�̂����ꂩ�ɂ���菇�͎��̗l�ɂȂ�B
�T�D�Ίp�s��ɕϊ����邽�߂̕ϊ��s��g�����߂�B

�@�@�@�mt�gt�`�g�m���v�Z����ƁA�Ίp�v�f��-�P�C�O�C�P�̂����ꂩ�ɂȂ�B �V�D�ϊ��s�͎��̗l�ɂȂ�B
�@�@�@�@�@�@�����g�m
�@�@�@��t�`���@���́@�`��'��'��������'������'�`�����@���v�Z����ƁA�Ίp�v�f��-�P�C�P�̑Ίp�s���܂�B
�y��̗�z
�T�D�Ίp�s��ɕϊ����邽�߂̕ϊ��s��g�����߂�B
�@�s��`���ŗL�l�����߂�B
�A�e�ŗL�l�ɑ����ŗL�x�N�g�������߂�B
�B�A���ŗL�x�N�g����P�ʃx�N�g��������B
�C�B�̃x�N�g�����x�N�g���Ƃ����ŗL�l�ɑΉ������ŗL�x�N�g���̐������A�ŗL�l�̏��������ɕ��ׂčs��g���쐬����B
�gt�`�g�͑Ίp�s��ɂȂ�B���̗v�f�͂`���ŗL�l�ł���B
�U�D�Ίp�v�f��-�P�C�O�C�P�̂����ꂩ�ɕϊ����邽�߂̕ϊ��s��m���A�e�ŗL�l�ɑ����ŗL�x�N�g�������߂�B
�B�A���ŗL�x�N�g����P�ʃx�N�g��������B
�C�B�̃x�N�g�����x�N�g���Ƃ����ŗL�l�ɑΉ������ŗL�x�N�g���̐������A�ŗL�l�̏��������ɕ��ׂčs��g���쐬����B
�gt�`�g�͑Ίp�s��ɂȂ�B���̗v�f�͂`���ŗL�l�ł���B

�@�@�@�mt�gt�`�g�m���v�Z����ƁA�Ίp�v�f��-�P�C�O�C�P�̂����ꂩ�ɂȂ�B �V�D�ϊ��s�͎��̗l�ɂȂ�B
�@�@�@�@�@�@�����g�m
�@�@�@��t�`���@���́@�`��'��'��������'������'�`�����@���v�Z����ƁA�Ίp�v�f��-�P�C�P�̑Ίp�s���܂�B
�y��̗�z
���L�̑Ώ̍s��`����ɏq�ׂ��菇�ŁA�`�̑Ίp�v�f��-�P�C�O�C�P�̑Ίp�s��ɕϊ�����s�����߂�B
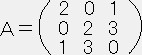
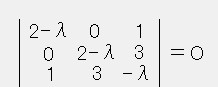
�ŗL�l�͏�̉E�̎����������ŋ��܂�B�ŗL�l�@��1���|�Q�D�R�P�V�C��2���Q�C��3���S�D�R�P�V
�ŗL�l�|�Q�D�R�P�V�ɑ����ŗL�x�N�g���̐������w�C�x�C�y�Ƃ����

 �@�x���R�w�C�@�y���|�S�D�R�P�V�w�C�@
�@�x���R�w�C�@�y���|�S�D�R�P�V�w�C�@
�]�����ŗL�l�|�Q�D�R�P�V�ɑΉ�����P�ʉ������ŗL�x�N�g���́@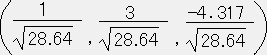
���l���ŗL�l�Q�ɑΉ�����P�ʉ������ŗL�x�N�g���́@�@�@�@�@�@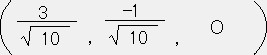
���l���ŗL�l�S�D�R�P�V�ɑΉ�����P�ʉ������ŗL�x�N�g���́@�@
�̂������s���g�y�эs��m��

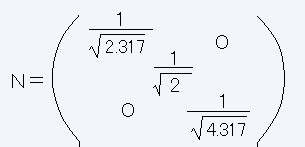
�ϊ��s��@�����g�m�@���v�Z�����

�ɂȂ�B��t�`���@���́@�`��'��'��������'������'�`�����@���v�Z����ƁA�Ίp�v�f��-�P�C�P�̑Ίp�s���܂�B
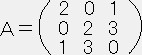
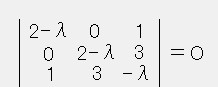
�ŗL�l�͏�̉E�̎����������ŋ��܂�B�ŗL�l�@��1���|�Q�D�R�P�V�C��2���Q�C��3���S�D�R�P�V
�ŗL�l�|�Q�D�R�P�V�ɑ����ŗL�x�N�g���̐������w�C�x�C�y�Ƃ����

 �@�x���R�w�C�@�y���|�S�D�R�P�V�w�C�@
�@�x���R�w�C�@�y���|�S�D�R�P�V�w�C�@
�]�����ŗL�l�|�Q�D�R�P�V�ɑΉ�����P�ʉ������ŗL�x�N�g���́@
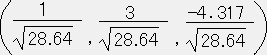
���l���ŗL�l�Q�ɑΉ�����P�ʉ������ŗL�x�N�g���́@�@�@�@�@�@
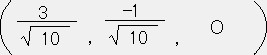
���l���ŗL�l�S�D�R�P�V�ɑΉ�����P�ʉ������ŗL�x�N�g���́@�@

�̂������s���g�y�эs��m��

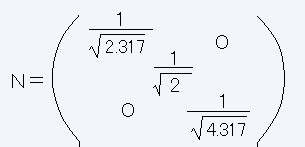
�ϊ��s��@�����g�m�@���v�Z�����

�ɂȂ�B��t�`���@���́@�`��'��'��������'������'�`�����@���v�Z����ƁA�Ίp�v�f��-�P�C�P�̑Ίp�s���܂�B
�t�^�Q�F�Ɨ��Ȑ����̐�
(1) ��2�w���^�݂w��'�݂w��'�̓Ɨ��Ȓl�̐��͂S�O
�i��' �C��'�j�̓Ɨ��ȃy�A�͉��L�̕\�̗l�ɂȂ�B
��̕\���A�g�ݍ��킹�̐��́@ ���i���{�P�j�@�@�����S������P�O��
���i���{�P�j�@�@�����S������P�O��
���͂S�̒l���Ƃ�邩��S���łS�O�̌W��������B
|
��̕\���A�g�ݍ��킹�̐��́@
 ���i���{�P�j�@�@�����S������P�O��
���i���{�P�j�@�@�����S������P�O�����͂S�̒l���Ƃ�邩��S���łS�O�̌W��������B
(2) ��3�w���^�݂w��'�݂w��'�݂w ��'�̓Ɨ��Ȓl�̐��͂W�O
�i��' �C��' �C��'�j�̓Ɨ��ȃy�A�͉��L�̕\�̗l�ɂȂ�B
��̕\���A�g�ݍ��킹�̐��́@
�@�@�@
�����S������i��' �C��' �C��'�j�̑Ώ̓I�ȑg�ݍ��킹�̐��͂Q�O��
���͂S�̒l��Ɨ��ɂƂ�邩��S���łW�O�̌W��������B
|
��̕\���A�g�ݍ��킹�̐��́@
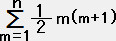
�@�@�@

�����S������i��' �C��' �C��'�j�̑Ώ̓I�ȑg�ݍ��킹�̐��͂Q�O��
���͂S�̒l��Ɨ��ɂƂ�邩��S���łW�O�̌W��������B
(3) �������C��'��'�̓Ɨ��Ȓl�̐��͂P�O�O
(�P)���i���C���j�ɑ��ĂP�O�́A�i��'�C��'�j�ɑ��ĂP�O�̂��ꂼ��ȃy�A������B�����̃y�A�݂͌��ɓƗ��ł��邩��A�P�O���P�O���P�O�O���Ɨ��ł���B
(�S) �q�����ʃ��̓Ɨ��Ȑ����̐��͂Q�P
�y�A�i���C���j�y�уy�A�i�ʁC�ˁj�͔��Ώ̂Ȃ̂ŁA���ꂼ�� ���� ���i���[�P�j �̓Ɨ��Ȑ��������B
���i���[�P�j �̓Ɨ��Ȑ��������B
�y�A�i���C���j�ƃy�A�i�ʁC�ˁj�͑Ώ̂Ȃ̂ŁA ���i���{�P�j �̓Ɨ��Ȑ��������B�����S ������ �����U
���i���{�P�j �̓Ɨ��Ȑ��������B�����S ������ �����U
����� �q�����ʃ� �� �Q�P�� �̓Ɨ��Ȑ����̐������B
 ���i���[�P�j �̓Ɨ��Ȑ��������B
���i���[�P�j �̓Ɨ��Ȑ��������B�y�A�i���C���j�ƃy�A�i�ʁC�ˁj�͑Ώ̂Ȃ̂ŁA
 ���i���{�P�j �̓Ɨ��Ȑ��������B�����S ������ �����U
���i���{�P�j �̓Ɨ��Ȑ��������B�����S ������ �����U����� �q�����ʃ� �� �Q�P�� �̓Ɨ��Ȑ����̐������B
�t�^�R�F�ȗ��Ɋւ�����̎���
���ʍ��W���ɉ����郊�[�}���ȗ��A���b�`�e���\���A���b�`�X�J���[���A�C���V���^�C���E�e���\���������ۂɌv�Z���Ă݂�B���[�}���ȗ����v�Z����ɂ̓N���X�g�b�t�F���L���Ƃ��̔������K�v�ł���B�N���X�g�b�t�F���L�����v�Z����ɂ́A���g���b�N�ƃ��g���b�N������������̂ƃ��g���b�N�̋t�s�K�v�ł���B�]���āA�悸���g���b�N���K�v�ł���B
(1) ���[�N���b�h���ʂł̋ɍ��W
�N���X�g�b�t�F���L�����Ȑ����W�n�@�U. �N���X�g�b�t�F���L���Ŋ��Ɍv�Z���Ă���̂ŁA������g�p����B
�@�@�@��r�ƃ� �� �|���@�C�@����r�� �� �@�C�@
������r ��
�@�C�@
������r �� 
�L���ȃN���X�g�b�t�F���L���͏�L�̎O�ŁA��͂O�ł���B���ŕΔ��������
�@�@�@��r�ƃƁCr �� �|�P�@�C�@����r�ƁCr �� �|�P�^��2�@�C�@ ���������Cr �� �|�P�^��2
���[�}���̋ȗ��e���\��
�@�@�@�q�����ʃ� �� �������ˁC���[ �������ʁC���{�����у����������[ �����у����������@�@�@�@ �ɉ����āA���C���C�ʁC�˂�r�y�уƂ������āA���[�}���̋ȗ��e���\���̐������v�Z����ƁA�S�ĂO�ɂȂ�B
���W�n�͋Ȑ����W�n�ł��邪���ʂ͕��R�ł��邩��A���[�}���̋ȗ��e���\���S�ĂO�ɂȂ�B���R�ȋ�Ԃł͂����鏊�� �����ʃ����O �ƂȂ�悤�ȍ��W�n�����݂��邪�A���̗�̂悤�� �����ʃ����O �ƂȂ���W�n��I�Ԏ����\�ł���B
�@�@�@
�@�@�@��r�ƃ� �� �|���@�C�@����r�� ��
 �@�C�@
������r ��
�@�C�@
������r �� 
�L���ȃN���X�g�b�t�F���L���͏�L�̎O�ŁA��͂O�ł���B���ŕΔ��������
�@�@�@��r�ƃƁCr �� �|�P�@�C�@����r�ƁCr �� �|�P�^��2�@�C�@ ���������Cr �� �|�P�^��2
���[�}���̋ȗ��e���\��
�@�@�@�q�����ʃ� �� �������ˁC���[ �������ʁC���{�����у����������[ �����у����������@�@�@�@ �ɉ����āA���C���C�ʁC�˂�r�y�уƂ������āA���[�}���̋ȗ��e���\���̐������v�Z����ƁA�S�ĂO�ɂȂ�B
���W�n�͋Ȑ����W�n�ł��邪���ʂ͕��R�ł��邩��A���[�}���̋ȗ��e���\���S�ĂO�ɂȂ�B���R�ȋ�Ԃł͂����鏊�� �����ʃ����O �ƂȂ�悤�ȍ��W�n�����݂��邪�A���̗�̂悤�� �����ʃ����O �ƂȂ���W�n��I�Ԏ����\�ł���B
�@�@�@
(2) �~���\�ʂ̃��[�}���ȗ��e���\��
�f�J���g���W�i�w�C�x�C�y�j�Ɖ~�����W�i���C�ƁC�y�j�Ƃ̊Ԃɂ͎��̊W������B
�@�@�@�w�����������Ɓ@�C�@�x�����������Ɓ@�C�@�y���y �]���ĕϊ��s�� ������' ��
�@�@�@�݂w�^�������������Ɓ@�@ �@�C�@�݂x�^�������������Ɓ@�@�C�@�݂y�^ �������O
�@�@�@�݂w�^�݃Ɓ�-���������Ɓ@�@�C�@�݂x�^�݃Ɓ����������Ɓ@�C�@�݂y�^�݃Ɓ��O
�@�@�@�݂w�^�݂y���O�@�@�@�@�@�@�@�C�@�݂x�^�݂y���O�@�@�@�@�@�C�@�݂y�^�݂y���P
�ȉ��A�ɍ��W�ł̃��g���b�N�����߂����Ɠ��l�ȕ��@�ʼn~�����W�ł̃��g���b�N���v�Z�����
�@�@�@��rr���P�@�C�@���ƃ�����2�@�C�@��zz���P�@�C�@���ƃƁCr���Q�� ���g���b�N�̋t�s���
�@�@�@��rr���P�@�C�@���ƃ����P�^��2�@�C�@��zz���P�@ �N���X�g�b�t�F���L�����v�Z����ƁA�L���ȃN���X�g�b�t�F���L����
�@�@�@��r�ƃ����[���@�C�@����r�����P�^���@�C�@ ������r���P�^��
���ŕΔ��������
�@�@�@��r�ƃƁCr �� �|�P�@�C�@����r�ƁCr �� �| �P�^��2�@�C�@ ������r�Cr �� �|�P�^��2
���[�}���̋ȗ��e���\��
�@�@�@�q�����ʃ� �� �������ˁC���[ ���� ���ʁC���{�����у����������[ �����у� ���������@�@�@�@ �ɉ����āA���C���C�ʁC�˂����C�Ƌy�тy�������āA���[�}���̋ȗ��e���\���̐������v�Z����ƁA�S�ĂO�ɂȂ�B
�~���\�ʂ͋Ȃ��Ă���l�ɂ݂��邪�A�~���\�ʂł̕��s���͂ǂ��܂ōs���Ă����s�ł��邩��A���[�}���̋ȗ��e���\���̐����͑S�ĂO�ɂȂ�B
�@�@�@�w�����������Ɓ@�C�@�x�����������Ɓ@�C�@�y���y �]���ĕϊ��s�� ������' ��
�@�@�@�݂w�^�������������Ɓ@�@ �@�C�@�݂x�^�������������Ɓ@�@�C�@�݂y�^ �������O
�@�@�@�݂w�^�݃Ɓ�-���������Ɓ@�@�C�@�݂x�^�݃Ɓ����������Ɓ@�C�@�݂y�^�݃Ɓ��O
�@�@�@�݂w�^�݂y���O�@�@�@�@�@�@�@�C�@�݂x�^�݂y���O�@�@�@�@�@�C�@�݂y�^�݂y���P
�ȉ��A�ɍ��W�ł̃��g���b�N�����߂����Ɠ��l�ȕ��@�ʼn~�����W�ł̃��g���b�N���v�Z�����
�@�@�@��rr���P�@�C�@���ƃ�����2�@�C�@��zz���P�@�C�@���ƃƁCr���Q�� ���g���b�N�̋t�s���
�@�@�@��rr���P�@�C�@���ƃ����P�^��2�@�C�@��zz���P�@ �N���X�g�b�t�F���L�����v�Z����ƁA�L���ȃN���X�g�b�t�F���L����
�@�@�@��r�ƃ����[���@�C�@����r�����P�^���@�C�@ ������r���P�^��
���ŕΔ��������
�@�@�@��r�ƃƁCr �� �|�P�@�C�@����r�ƁCr �� �| �P�^��2�@�C�@ ������r�Cr �� �|�P�^��2
���[�}���̋ȗ��e���\��
�@�@�@�q�����ʃ� �� �������ˁC���[ ���� ���ʁC���{�����у����������[ �����у� ���������@�@�@�@ �ɉ����āA���C���C�ʁC�˂����C�Ƌy�тy�������āA���[�}���̋ȗ��e���\���̐������v�Z����ƁA�S�ĂO�ɂȂ�B
�~���\�ʂ͋Ȃ��Ă���l�ɂ݂��邪�A�~���\�ʂł̕��s���͂ǂ��܂ōs���Ă����s�ł��邩��A���[�}���̋ȗ��e���\���̐����͑S�ĂO�ɂȂ�B
(3) ���a�����̋��̋ɍ��W�ł̋ȗ��Ɋւ�����
�f�J���g���W�i�w�C�x�C�y�j�Ƌ��ʍ��W�i���C�ƁC���j�Ƃ̊Ԃɂ͎��̊W������B
�@�@�@�w���������������������@�C�@�x���������������������@�C�@�y������������ �ɍ��W�ł̃��g���b�N�����߂����Ɠ��l�ȕ��@�ŁA�ϊ��s�� ������' �����߁A�ɍ��W�ł̃��g���b�N���v�Z�����
�@�@�@���ƃ�����2�@�C�@���Ӄ�����2������2�Ɓ@�C�@���Ӄ��C�����Q��2���������������� ���g���b�N�̋t�s���
�@�@�@���ƃ����P�^��2�@�C�@���Ӄ����P�^��2������2�Ɓ@ �N���X�g�b�t�F���L�����v�Z����ƁA�L���ȃN���X�g�b�t�F���L����
�@�@�@�����Ӄ���-���������������Ɓ@�C�@�����������������Ɓ^�������Ɓ@�C�@ �����������������Ɓ^��������
�ƂŕΔ��������
�@�@�@�����Ӄ��C�� �� 2������2��-1�@�C�@���������C�� �� �| �P�^������2�Ɓ@�C�@ �������ƁC�� �� �|�P�^������2��
���[�}���̋ȗ��e���\��
�@�@�@�q�����ʃ� �� �������ˁC���[ ���� ���ʁC���{�����у����������[ �����у� ���������@�@�@�@ �ɉ����āA���C���C�ʁC�˂ɃƋy�����������āA���[�}���̋ȗ��e���\���̐������v�Z����ƁA�L���Ȑ�����
�@�@�@�E�@�q�������� �� ������2�Ɓ@�C�@�q���Ӄ��� �� -������2�Ɓ@�C�@�q���ƃ��� �� -�P�@�C�@�q�������� �� �P
���[�}���̋ȗ��e���\���̑��Ƒ�O�̓Y�����k�ē��������b�`�e���\���́A�L���Ȑ�����
�@�@�@�E�@�q�b�g�ƃ� �� �P�@�C�@�q�b�g�Ӄ� �� ������2��
���b�`�X�J���[�i���q�r�b�`�k�`�q�j�����߂鎮 �q�r�b�`�k�`�q�����ʃ��q�b�g�ʃ� �ɂ��A���b�`�X�J���[���v�Z�����
�@�@�@�E�@�q�r�b�`�k�`�q �� �Q�^��2
�@�@�@�w���������������������@�C�@�x���������������������@�C�@�y������������ �ɍ��W�ł̃��g���b�N�����߂����Ɠ��l�ȕ��@�ŁA�ϊ��s�� ������' �����߁A�ɍ��W�ł̃��g���b�N���v�Z�����
�@�@�@���ƃ�����2�@�C�@���Ӄ�����2������2�Ɓ@�C�@���Ӄ��C�����Q��2���������������� ���g���b�N�̋t�s���
�@�@�@���ƃ����P�^��2�@�C�@���Ӄ����P�^��2������2�Ɓ@ �N���X�g�b�t�F���L�����v�Z����ƁA�L���ȃN���X�g�b�t�F���L����
�@�@�@�����Ӄ���-���������������Ɓ@�C�@�����������������Ɓ^�������Ɓ@�C�@ �����������������Ɓ^��������
�ƂŕΔ��������
�@�@�@�����Ӄ��C�� �� 2������2��-1�@�C�@���������C�� �� �| �P�^������2�Ɓ@�C�@ �������ƁC�� �� �|�P�^������2��
���[�}���̋ȗ��e���\��
�@�@�@�q�����ʃ� �� �������ˁC���[ ���� ���ʁC���{�����у����������[ �����у� ���������@�@�@�@ �ɉ����āA���C���C�ʁC�˂ɃƋy�����������āA���[�}���̋ȗ��e���\���̐������v�Z����ƁA�L���Ȑ�����
�@�@�@�E�@�q�������� �� ������2�Ɓ@�C�@�q���Ӄ��� �� -������2�Ɓ@�C�@�q���ƃ��� �� -�P�@�C�@�q�������� �� �P
���[�}���̋ȗ��e���\���̑��Ƒ�O�̓Y�����k�ē��������b�`�e���\���́A�L���Ȑ�����
�@�@�@�E�@�q�b�g�ƃ� �� �P�@�C�@�q�b�g�Ӄ� �� ������2��
���b�`�X�J���[�i���q�r�b�`�k�`�q�j�����߂鎮 �q�r�b�`�k�`�q�����ʃ��q�b�g�ʃ� �ɂ��A���b�`�X�J���[���v�Z�����
�@�@�@�E�@�q�r�b�`�k�`�q �� �Q�^��2
(4) ���v�f�����L�̂悤�ȑ��l�̂̋ȗ��Ɋւ�����
�@�@�@����2��-��2������2�{��2������2�{��2�i����2�{������2������2�j
���g���b�N��
�@�@�@��tt��-��2���@�C�@��rr����2���@�C�@���ƃ�����2�@�C�@���Ӄ�����2������2�� ���g���b�N�̋t�s���
�@�@�@��tt��-�P�^��2���@�C�@��rr���P�^��2���@�C�@���ƃ����P�^��2�@�C�@���Ӄ����P�^�i��2������2�Ɓj ���g���b�N�����y�уƂŕΔ����i ' �����ŕΔ�����������\���B �j
�@�@�@��tt�C����-2��2����'�@�C�@��rr�C����2�� 2����'�@�C�@���ƃƁC�����Q��
�@�@�@���Ӄ��C�����Q��������2�Ɓ@�C�@���Ӄ��C�����Q�� 2���������������� �N���X�g�b�t�F���L�����v�Z����ƁA�L���ȃN���X�g�b�t�F���L����
�@�@�@��ttr����'�@�C�@��trt����'
�@�@�@��rtt����2��-2����'�@�C�@��rrr����'�@�C�@��r�ƃ���-����-2���@�C�@��r�Ӄ���-��������2����-2��
�@�@�@����r�����P�^���@�C�@������r���P�^���@�C�@�����Ӄ���-����������������
�@�@�@����r�����P�^���@�C�@������r���P�^���@�C�@�����������������Ɓ^�������Ɓ@�C�@�����������������Ɓ^�������� �N���X�g�b�t�F���L�������y�уƂŕΔ��������
�@�@�@��ttr�C������''�@�C�@��trt�C������''
�@�@�@��rtt�C�����Q��2��-2���i��'-��'�j��'�{��2��-2����''�@�C �@��rrr�C������''
�@�@�@��r�ƃƁC����-��-2���{�Q����-2����'�@�C�@ ��r�Ӄ��C����-������2����-2���{�Q��������2����-2�� ��'
�@�@�@��r�Ӄ��C����-�Q��������������������-2��
�@�@�@����r�ƁC����-�P�^��2�@�C�@������r�C����-�P�^�� 2�@�C�@�����Ӄ��C�����Q������2��-�P
�@�@�@���������C����-�P�^��2�@�C�@�����ӂ��C����-�P�^�� 2�@�C�@���������C����-�P�^������2�Ɓ@�C�@�������ƁC�� ��-�P�^������2��
���[�}���̋ȗ��e���\��
�@�@�@�q�����ʃ� �� �������ˁC���[ ���� ���ʁC���{�����у����������[ �����у� ���������@�@�@�@ �ɉ����āA���C���C�ʁC�˂����C���C�Ƌy�����������Čv�Z����B���ʂ����[�}���̋ȗ��e���\���̐������Q�ƁB
���[�}���̋ȗ��e���\���̑��Ƒ�O�̓Y�����k�ē��������b�`�e���\���́A�L���Ȑ��� ��
�@�@�@�E�@�q�b�gtt �� ��2��-2���i��''�{�i��'�j2-��'��'�{�Q��'�^���j
�@�@�@�E�@�q�b�grr �� -��''-�i��'�j2�{��'��'�{�Q��'�^��
�@�@�@�E�@�q�b�g�ƃ� �� �P�|��-2���|����-2����'�{�� ��-2����'
�@�@�@�E�@�q�b�g�Ӄ� �� ������2�Ƃq�b�g�ƃ�
���b�`�X�J���[�i���q�r�b�`�k�`�q�j�����߂鎮 �q�r�b�`�k�`�q�����ʃ��q�b�g �ʃ� �ɂ��A���b�`�X�J���[���v�Z�����
�@�@�@�E�@�q�r�b�`�k�`�q �� �[�Q��-2���i��''�{�i��'�j2-��'��'�{��'�^ ���[��'�^���j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�Q�i�P�|��-2���|����-2����'�{���� -2����'�j�^��2 �A�C���V���^�C���E�e���\����
�@�@�@�E�@�ftt �� �i���[����-2���j
�i���[����-2���j
�@�@�@�E�@�frr �� �[��2���^��2�{�P�^��2�{�Q��'�^��
�@�@�@�E�@�f�ƃ� �� ��2��-2���i��''�{�i��'�j2-��'��'�{��'�^ ���[��'�^���j
�@�@�@�E�@�f�Ӄ� �� ������2�Ƃf�ƃ�
�@�@�@��tt��-��2���@�C�@��rr����2���@�C�@���ƃ�����2�@�C�@���Ӄ�����2������2�� ���g���b�N�̋t�s���
�@�@�@��tt��-�P�^��2���@�C�@��rr���P�^��2���@�C�@���ƃ����P�^��2�@�C�@���Ӄ����P�^�i��2������2�Ɓj ���g���b�N�����y�уƂŕΔ����i ' �����ŕΔ�����������\���B �j
�@�@�@��tt�C����-2��2����'�@�C�@��rr�C����2�� 2����'�@�C�@���ƃƁC�����Q��
�@�@�@���Ӄ��C�����Q��������2�Ɓ@�C�@���Ӄ��C�����Q�� 2���������������� �N���X�g�b�t�F���L�����v�Z����ƁA�L���ȃN���X�g�b�t�F���L����
�@�@�@��ttr����'�@�C�@��trt����'
�@�@�@��rtt����2��-2����'�@�C�@��rrr����'�@�C�@��r�ƃ���-����-2���@�C�@��r�Ӄ���-��������2����-2��
�@�@�@����r�����P�^���@�C�@������r���P�^���@�C�@�����Ӄ���-����������������
�@�@�@����r�����P�^���@�C�@������r���P�^���@�C�@�����������������Ɓ^�������Ɓ@�C�@�����������������Ɓ^�������� �N���X�g�b�t�F���L�������y�уƂŕΔ��������
�@�@�@��ttr�C������''�@�C�@��trt�C������''
�@�@�@��rtt�C�����Q��2��-2���i��'-��'�j��'�{��2��-2����''�@�C �@��rrr�C������''
�@�@�@��r�ƃƁC����-��-2���{�Q����-2����'�@�C�@ ��r�Ӄ��C����-������2����-2���{�Q��������2����-2�� ��'
�@�@�@��r�Ӄ��C����-�Q��������������������-2��
�@�@�@����r�ƁC����-�P�^��2�@�C�@������r�C����-�P�^�� 2�@�C�@�����Ӄ��C�����Q������2��-�P
�@�@�@���������C����-�P�^��2�@�C�@�����ӂ��C����-�P�^�� 2�@�C�@���������C����-�P�^������2�Ɓ@�C�@�������ƁC�� ��-�P�^������2��
���[�}���̋ȗ��e���\��
�@�@�@�q�����ʃ� �� �������ˁC���[ ���� ���ʁC���{�����у����������[ �����у� ���������@�@�@�@ �ɉ����āA���C���C�ʁC�˂����C���C�Ƌy�����������Čv�Z����B���ʂ����[�}���̋ȗ��e���\���̐������Q�ƁB
���[�}���̋ȗ��e���\���̑��Ƒ�O�̓Y�����k�ē��������b�`�e���\���́A�L���Ȑ��� ��
�@�@�@�E�@�q�b�gtt �� ��2��-2���i��''�{�i��'�j2-��'��'�{�Q��'�^���j
�@�@�@�E�@�q�b�grr �� -��''-�i��'�j2�{��'��'�{�Q��'�^��
�@�@�@�E�@�q�b�g�ƃ� �� �P�|��-2���|����-2����'�{�� ��-2����'
�@�@�@�E�@�q�b�g�Ӄ� �� ������2�Ƃq�b�g�ƃ�
���b�`�X�J���[�i���q�r�b�`�k�`�q�j�����߂鎮 �q�r�b�`�k�`�q�����ʃ��q�b�g �ʃ� �ɂ��A���b�`�X�J���[���v�Z�����
�@�@�@�E�@�q�r�b�`�k�`�q �� �[�Q��-2���i��''�{�i��'�j2-��'��'�{��'�^ ���[��'�^���j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�Q�i�P�|��-2���|����-2����'�{���� -2����'�j�^��2 �A�C���V���^�C���E�e���\����
�@�@�@�E�@�ftt ��
 �i���[����-2���j
�i���[����-2���j�@�@�@�E�@�frr �� �[��2���^��2�{�P�^��2�{�Q��'�^��
�@�@�@�E�@�f�ƃ� �� ��2��-2���i��''�{�i��'�j2-��'��'�{��'�^ ���[��'�^���j
�@�@�@�E�@�f�Ӄ� �� ������2�Ƃf�ƃ�
�t�^�S�F�s�̔���
�s�����̗]�������������A�s���������̋t�s����������Ƃ���Ǝ��̊W������B
�@�@�@���������������^���@ �@ ����������������
�s�����͗]�������������g����
�@ ����������������
�s�����͗]�������������g����
�@�@�@��������1����1�{�c�{������������ �{�c�{����n����n �ƕ\����B��̎����������ŕΔ��������
�@�@�@ ������������������
���ӂ�
������������������
���ӂ� 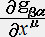 �@���|�����
�@���|�����
�@�@�@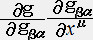 ����������
����������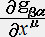 �@�@
�@�@ �@�@
�@�@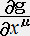 ����������
����������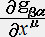 �@�@�@���@��,������������������,��
�@�@�@���@��,������������������,��
�@�@�@���������������^���@
 �@ ����������������
�s�����͗]�������������g����
�@ ����������������
�s�����͗]�������������g�����@�@�@��������1����1�{�c�{������������ �{�c�{����n����n �ƕ\����B��̎����������ŕΔ��������
�@�@�@
 ������������������
���ӂ�
������������������
���ӂ� 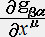 �@���|�����
�@���|������@�@�@
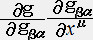 ����������
����������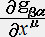 �@�@
�@�@ �@�@
�@�@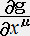 ����������
����������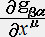 �@�@�@���@��,������������������,��
�@�@�@���@��,������������������,��