���Θ_�ɉ����闬��
< �ڎ��� >
���̏͂ł͈�ʑ��ΐ����_�ɉ�����A�C���V���^�C���̏d�͏�̕������̉E�ӂɂɏo�Ă��邱�G�l���M�[�^���ʃe���\���ɂ��ďq�ׂ�B�d�͏�̕�������
�@�@�@�@�@�q�ʃ��|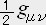 �q���|���s�ʃ�
�q���|���s�ʃ�
�Ƃ����`�ŕ\������P�O���A���Q�K����`�̕Δ����������ŁA���g���b�N�e���\�� �� �����߂���̂ł���B�E�ӂ͏d�͂̌��ɂȂ镨���̃G�l���M�[�^���ʃe���\���i���s�j�ł���B���ӂ͎���̂䂪�݂�\�����ŁA����������̂䂪�݂̌����ɂȂ�Ɖ��ߏo����B
�@�@�@�@�@�q�ʃ��|
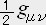 �q���|���s�ʃ�
�q���|���s�ʃ�
�P�D���@�@�@�@�@�@��
�����͉��x�ɂ���Čő́A�t�́A�C�̂̎O�̏�Ԃ�����B�t�̂ƋC�̂͗����������_���炷��悭���Ă��葍�̂��ė��̂ƌĂԁB�����Ă��̌ő̂͏\���ɍ������͉��ł͗����悤�ɂȂ�̂ň�ʑ��Θ_�I�V�̕����w�ɉ����ẮA�d�͌��͊��S���̂Ƃ��Ă悢�B���S���̂Ƃ͉^�����Ă��鎞�ł��A�����̖ʂɈ��͂�����p���Ȃ����̂̂��Ƃł���B���̂͂���߂đ����̗��q�̏W���̂ł����āA�e���q�̉^���ׂ鎖�͕s�\�ł���B���̂��ߒP�ʑ̐ς�����̗��q���A�G�l���M�[���x�A�^���ʖ��x�A���́A���x�Ƃ������ʂ̕��ϗʂɂ���Ă��̏W���̂̏�Ԃ��L�q���邵���Ȃ��B
�Q�D�d�@�́@��@�́@��
�j���[�g�����_�ł͏d�͏�̌��͎��ʖ��x�����ł������B�A�C���V���^�C���́A���ʖ��x�i���G�l���M�[�j�����łȂ��A�X�g���X�i�����́j�A�^���ʂ��d�͏�̌��ƂȂ�A��Ԃ��Ȃ��錴���ƂȂ鎖�𑊑ΐ����_�ɉ����Ď������B���ʖ��x�A�X�g���X�A�^���ʂ��܂�
�߂ăe���\���ɂ����̂��X�g���X�[�G�l���M�[�e���\���ł���B���ʂ̏ł͎��ʖ��x >> �X�g���X�ł��邪�A���ɍ����x�̕����i�����q���j����ȍ����̂��ߗ��q�������ɋ߂����x�ʼn^�����Ă��镨���i���Θ_�I�K�X�j�ł͎��ʖ��x  �X�g���X�ƂȂ�B
�X�g���X�ƂȂ�B
 �X�g���X�ƂȂ�B
�X�g���X�ƂȂ�B
�R�D�_�@�X�@�g
�ł��P���ȗ��́A�_�X�g�𑊑Θ_�I�Ɏ�舵���B�_�X�g�Ƃ͂����̃��[�����c�n�Ő��~���Ă��闱�q�̏W���̎��ł���B
(1) ���q�����x
���q�����x�Ƃ͒P�ʑ̐ς�����̗��q���̎��ł���B���q�̐Î~�n�i�l�b�q�n���n �j�ł͒P���ɗ��q�̐��i�����j�ł��邪�A���q�̐Î~���Ă��Ȃ��nS�ł͗��q�����x�����ł͂Ȃ��B���q�����l�b�q�n���nS�������ł��邪�A�nS�ł����[�����c���k�ɂ�藱�q�̉^�������̒�����
�j�ł͒P���ɗ��q�̐��i�����j�ł��邪�A���q�̐Î~���Ă��Ȃ��nS�ł͗��q�����x�����ł͂Ȃ��B���q�����l�b�q�n���nS�������ł��邪�A�nS�ł����[�����c���k�ɂ�藱�q�̉^�������̒����� �{�����Z���Ȃ�̂ŗ��q�����x�����^
�{�����Z���Ȃ�̂ŗ��q�����x�����^ �ƂȂ�B
�ƂȂ�B
�@�@�@���q�����x�����^
 �j�ł͒P���ɗ��q�̐��i�����j�ł��邪�A���q�̐Î~���Ă��Ȃ��nS�ł͗��q�����x�����ł͂Ȃ��B���q�����l�b�q�n���nS�������ł��邪�A�nS�ł����[�����c���k�ɂ�藱�q�̉^�������̒�����
�j�ł͒P���ɗ��q�̐��i�����j�ł��邪�A���q�̐Î~���Ă��Ȃ��nS�ł͗��q�����x�����ł͂Ȃ��B���q�����l�b�q�n���nS�������ł��邪�A�nS�ł����[�����c���k�ɂ�藱�q�̉^�������̒����� �{�����Z���Ȃ�̂ŗ��q�����x�����^
�{�����Z���Ȃ�̂ŗ��q�����x�����^ �ƂȂ�B
�ƂȂ�B�@�@�@���q�����x�����^

(2) ���@�@��
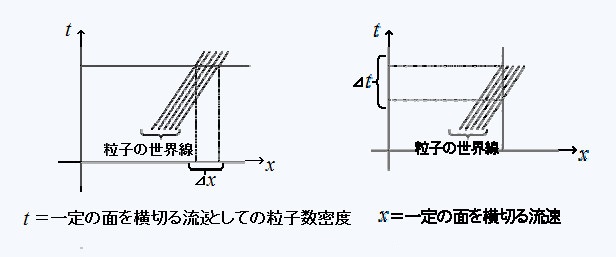
����ʂ����闱�q�̗����Ƃ́A�P�ʎ��Ԃ����肻�̖ʂ̒P�ʖʐς����闱�q���̂��Ƃł���B���q�̐Î~�n�ł́A�S�Ă̗��q���Î~���Ă���̂����痬���̓[���ł���B�nS�őS�Ă̗��q���w�����ɑ��x�u�ʼn^�����Ă���Ƃ���ƁA�w�����̖ʂ����闬����
�@�@�@���������q�����x �� �u�����u�^
���x�u���w�����łȂ��A�u�̂w�����̐������u���Ȃ�A�w�����̖ʂ����闬����
�@�@�@���������u���^ �ƂȂ�B
�ƂȂ�B
�����ɂ��A���錈�܂��������ɂǂꂾ���̗��q���^�����Ă��邩��������B
�@�@�@���������q�����x �� �u�����u�^

���x�u���w�����łȂ��A�u�̂w�����̐������u���Ȃ�A�w�����̖ʂ����闬����
�@�@�@���������u���^
 �ƂȂ�B
�ƂȂ�B(�R) �l������
���q�����x�A�����̐������l������ 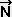 �����̗l�ɒ�`�o����B�i�l���^�������`�������Ɠ����v�́j
�����̗l�ɒ�`�o����B�i�l���^�������`�������Ɠ����v�́j
�@�@�@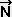 ����
���� �@ �i �Î~�n�ɉ����闱�q�� �� �l�����x �j
�@ �i �Î~�n�ɉ����闱�q�� �� �l�����x �j
�nS�ɉ����鐬���� 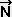 ���i �m0�C�m1�C�m2�C�m3 �j �Ƃ����
���i �m0�C�m1�C�m2�C�m3 �j �Ƃ����
�@�@�@�m0��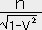 , �@�m1��
, �@�m1��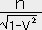 �u�� , �@�m2��
�u�� , �@�m2��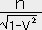 �u�� , �@�m3��
�u�� , �@�m3��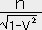 �u��
�u��
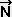 �̎��Ԑ����͗��q�����x�ŁA��Ԑ����͂��ꂼ��̍��W���ɐ����Ȗʂ����闬����\���Ă���B
�̎��Ԑ����͗��q�����x�ŁA��Ԑ����͂��ꂼ��̍��W���ɐ����Ȗʂ����闬����\���Ă���B
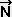 �����̗l�ɒ�`�o����B�i�l���^�������`�������Ɠ����v�́j
�����̗l�ɒ�`�o����B�i�l���^�������`�������Ɠ����v�́j�@�@�@
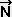 ����
���� �@ �i �Î~�n�ɉ����闱�q�� �� �l�����x �j
�@ �i �Î~�n�ɉ����闱�q�� �� �l�����x �j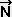 ���i �m0�C�m1�C�m2�C�m3 �j �Ƃ����
���i �m0�C�m1�C�m2�C�m3 �j �Ƃ����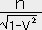 , �@�m1��
, �@�m1��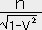 �u�� , �@�m2��
�u�� , �@�m2��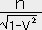 �u�� , �@�m3��
�u�� , �@�m3��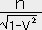 �u��
�u��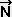 �̎��Ԑ����͗��q�����x�ŁA��Ԑ����͂��ꂼ��̍��W���ɐ����Ȗʂ����闬����\���Ă���B
�̎��Ԑ����͗��q�����x�ŁA��Ԑ����͂��ꂼ��̍��W���ɐ����Ȗʂ����闬����\���Ă���B
�S�D�_�X�g�̃X�g���X�[�G�l���M�[�e���\��
�R. �Ń_�X�g�̌��ɂ��Ē��ׂ����_�X�g�̓G�l���M�[���^���ʂ����B�X�g���X�i�����́j�͂Ȃ��B�i�����̃��[�����c�n�Ő��~���Ă���ׁj
(1) �G�l���M�[���x�A�^���ʖ��x
�l�b�q�n�ł́A�e���q�̃G�l���M�[�����i���Î~���ʁj�ŁA�P�ʑ̐ς�����̌������ł���������A�P�ʑ̐ς�����̃G�l���M�[�i���G�l���M�[���x�j�͂����ł���B�������ʂ� �� �ŕ\���B
�@�@�@�� �� �����@�@�i�@���̎��͈�ʂ̗��̂̏ꍇ�ɂ͕��ϓI�ȐÎ~�n���Ƃ��Ă����藧���Ȃ��B�@�j
�ϑ��҂̌nS�ł͊e���q�̃G�l���M�[�� ���^ �i���l���^���ʂ̎��Ԑ����j�A���q�����x�� ���^
�i���l���^���ʂ̎��Ԑ����j�A���q�����x�� ���^ �i���l�������̎��Ԑ����j�ł���B
�]���ăG�l���M�[���x�� �����^(�P�|�u�Q�j�ƂȂ�B�^���ʖ��x�i���P�ʑ̐ς�����̉^���ʁj�����l�ȕ��@�Łi���l���^���ʂ̋�Ԑ��� x �l�������̋�Ԑ����j���߂鎖���o����B
�i���l�������̎��Ԑ����j�ł���B
�]���ăG�l���M�[���x�� �����^(�P�|�u�Q�j�ƂȂ�B�^���ʖ��x�i���P�ʑ̐ς�����̉^���ʁj�����l�ȕ��@�Łi���l���^���ʂ̋�Ԑ��� x �l�������̋�Ԑ����j���߂鎖���o����B
�@�@�@�� �� �����@�@�i�@���̎��͈�ʂ̗��̂̏ꍇ�ɂ͕��ϓI�ȐÎ~�n���Ƃ��Ă����藧���Ȃ��B�@�j
 �i���l���^���ʂ̎��Ԑ����j�A���q�����x�� ���^
�i���l���^���ʂ̎��Ԑ����j�A���q�����x�� ���^ �i���l�������̎��Ԑ����j�ł���B
�]���ăG�l���M�[���x�� �����^(�P�|�u�Q�j�ƂȂ�B�^���ʖ��x�i���P�ʑ̐ς�����̉^���ʁj�����l�ȕ��@�Łi���l���^���ʂ̋�Ԑ��� x �l�������̋�Ԑ����j���߂鎖���o����B
�i���l�������̎��Ԑ����j�ł���B
�]���ăG�l���M�[���x�� �����^(�P�|�u�Q�j�ƂȂ�B�^���ʖ��x�i���P�ʑ̐ς�����̉^���ʁj�����l�ȕ��@�Łi���l���^���ʂ̋�Ԑ��� x �l�������̋�Ԑ����j���߂鎖���o����B
(2) �X�g���X�[�G�l���M�[�e���\��
�X�g���X�[�G�l���M�[�e���\�����`����̂ɍł��֗��Ȃ̂́A����C�ӂ̌n�ł̐������g�����Ƃł���B
�@�@�@�s�i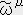 �C
�C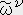 �j �� �s�ʃ� �� �w�����̖ʂ�����ʉ^���ʗ���
�j �� �s�ʃ� �� �w�����̖ʂ�����ʉ^���ʗ���
�s�ɂ͓�̈�`�����ϐ��Ƃ��ĕK�v�ł���B��͉^���ʗ������`���邽�߂ɁA������͖ʂ��`���邽�߂ł���B
�@�@�@�@�@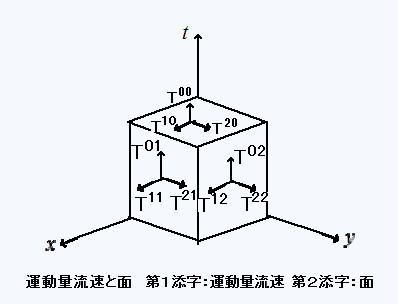
�y�s�ʃ��̏ڍא����z
�@�@�E �s00���G�l���M�[���x
�@�@�@�@ �������̖ʂ�����O�^���ʁi���G�l���M�[�j�̗���
�@�@�E �s0���������ʂ�����G�l���M�[�����@�@�i����1�` 3�j
�@�@�@�@ ���������̖ʂ�����G�l���M�[����
�@�@�E �s��0�����^���ʖ��x�@�@�i����1�` 3�j
�@�@�@�@ �������̖ʂ��������^���ʗ���
�@�@�E �s�����������ʂ��������^���ʗ����@�@�i ���C����1�` 3 �j
�@�@�@�@ ���^���ʂ�������
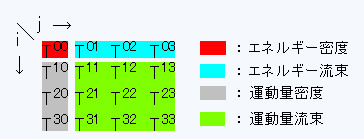
(1)�y�шȏ�̂��Ƃ�莟�̎���������B
�@�@�@�_�X�g�F�s ��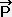
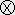
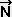 �� ����
�� ����
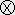
 �� ��
�� ��
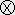
 �� ���t���t��
�� ���t���t�� 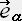
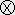
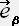
�@�@�@ �����t���t��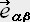
�s���e���\���ł��鎖�̏ؖ����Q�̃x�N�g���̐����̒��ϗʂ̓e���V�����Q�ƁB
�s�̐�����
�@�@�@�s�ʃ� �� �s�i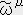 �C
�C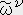 �j �� ���t���t��
�j �� ���t���t��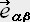 �i
�i 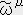 �C
�C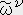 �j
�� ���t���t��
�j
�� ���t���t��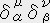 �@�i��`���̊�����Q�Ɓj
�@�i��`���̊�����Q�Ɓj
�@�@�@�@�@�@ �����t���t��
�_�X�g���l�b�q�n�ł� ���q�̉^�����Ȃ��̂őS�Ă̗����̋�Ԑ����̓[���ƂȂ�B�܂�
�s00 �� �� �ő��̐����͑S�ĂO�ł���B
�@�@�@�s�i
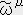 �C
�C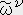 �j �� �s�ʃ� �� �w�����̖ʂ�����ʉ^���ʗ���
�j �� �s�ʃ� �� �w�����̖ʂ�����ʉ^���ʗ����@�@�@�@�@

�@�@�E �s00���G�l���M�[���x
�@�@�@�@ �������̖ʂ�����O�^���ʁi���G�l���M�[�j�̗���
�@�@�@�@ ���������̖ʂ�����G�l���M�[����
�@�@�@�@ �������̖ʂ��������^���ʗ���
�@�@�@�@ ���^���ʂ�������

(1)�y�шȏ�̂��Ƃ�莟�̎���������B
�@�@�@�_�X�g�F�s ��
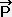
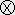
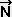 �� ����
�� ����
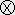
 �� ��
�� ��
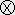
 �� ���t���t��
�� ���t���t�� 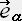
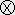
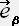
�@�@�@ �����t���t��
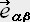
�s�̐�����
�@�@�@�s�ʃ� �� �s�i
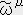 �C
�C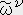 �j �� ���t���t��
�j �� ���t���t��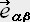 �i
�i 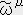 �C
�C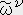 �j
�� ���t���t��
�j
�� ���t���t��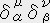 �@�i��`���̊�����Q�Ɓj
�@�i��`���̊�����Q�Ɓj
�@�@�@�@�@�@ �����t���t��
�s00 �� �� �ő��̐����͑S�ĂO�ł���B
�T�D��@�ʁ@�́@���@��
�_�X�g�͗��q�̏W���Ƃ��Ă͈�ԊȒP�ȏꍇ�ł������B ��ʂ̗��̂ł́A�@���̂̑S�̂̉^���̂ق��ɁA�e���q�������_���ȉ^�������Ă���B�A���q�Ԃ̂��܂��܂ȗ͂������āA����̓|�e���V�����G�l���M�[�̌`�œ����Ă���B�̓�̏������͓����Ă���B
(1) �X�g���X�[�G�l���M�[�e���\��
�S. (2)�ɉ����鎮�́i�����L�̎��j���S�Ɉ�ʓI�Ȃ��̂ł���B
�@�@�@�s�i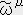 �C
�C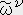 �j �� �s�ʃ� �� �w�����̖ʂ�����ʉ^���ʗ���
�j �� �s�ʃ� �� �w�����̖ʂ�����ʉ^���ʗ���
��̗ʂ�MCR�n�Ō��Ă݂�BMCR�n�ł͗��̗v�f�̑S�̓I�ȉ^���͂Ȃ����A���q�̋�Ԑ������Ȃ��B
�]�����l�b�q�n�ł�
�@�@�E �s00���G�l���M�[���x����
�@�@�E �s0�����G�l���M�[�����B�^���͂Ȃ����A�G�l���M�[�͔M�`���A�����꓾��B�@�@ �i����1�` 3�j
�@�@�E �s��0���^���ʖ��x�B���q�͂�͂�^���ʂ������Ȃ����A�M���`���ƃG�l���M�[�͉^���ʂ��^�ԁB
�@�@�@�@�@�@�@�@�@�s��0���s0���ƂȂ�B�@�i����1�` 3�j
�@�@�E �s�������^���ʗ����B������X�g���X�Ƃ����B�i�����́A���́j
�y�s�̋�Ԑ����s�����z
�@�@�E�@�s0�� �� �s��0
�@�@�@�s�i
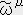 �C
�C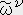 �j �� �s�ʃ� �� �w�����̖ʂ�����ʉ^���ʗ���
�j �� �s�ʃ� �� �w�����̖ʂ�����ʉ^���ʗ����]�����l�b�q�n�ł�
�@�@�E �s0�����G�l���M�[�����B�^���͂Ȃ����A�G�l���M�[�͔M�`���A�����꓾��B�@�@ �i����1�` 3�j
�@�@�E �s��0���^���ʖ��x�B���q�͂�͂�^���ʂ������Ȃ����A�M���`���ƃG�l���M�[�͉^���ʂ��^�ԁB
�@�@�@�@�@�@�@�@�@�s��0���s0���ƂȂ�B�@�i����1�` 3�j
�@�@�E �s�������^���ʗ����B������X�g���X�Ƃ����B�i�����́A���́j
�y�s�̋�Ԑ����s�����z
�s���������ʂ��������^���ʗ����ł���B���l�b�q�n���l���Ă���̂ŁA���̗v�f�̑S�̓I�ȉ^���͂Ȃ����X�g���X�͂���B
���̂̓����Ɉ�̖ʃĂ��l���A���̃Ăŗ��̂��̕����`�Ƃa�ɕ�����i���̐}�Q�Ɓj�B
��ʂɂ͂`�Ƃa�͑��݂ɗ͂��y�ڂ������Ă���B�s�����͂��̗́i���X�g���X�j�̎��ł���B�͂��ʂɐ����Ȃ�s�������������̎��̓[���ɂȂ�B
�@�@�@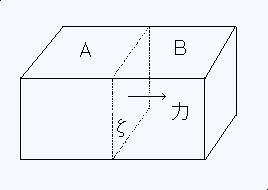
�y�l�b�q�n�ł̂s�����̑Ώ̐��z ���̂̓����Ɉ�̖ʃĂ��l���A���̃Ăŗ��̂��̕����`�Ƃa�ɕ�����i���̐}�Q�Ɓj�B
��ʂɂ͂`�Ƃa�͑��݂ɗ͂��y�ڂ������Ă���B�s�����͂��̗́i���X�g���X�j�̎��ł���B�͂��ʂɐ����Ȃ�s�������������̎��̓[���ɂȂ�B
�@�@�@

�@�@�E�@�s0�� �� �s��0
�s0���̓G�l���M�[�����ŁA�s��0�͉^���ʖ��x�ł���B
�G�l���M�[�������G�l���M�[���x�����̗���̑��x�ł��邪�A�G�l���M�[�Ǝ��ʂ͓����ł��邩��G�l���M�[���������ʖ��x�����̗���̑��x�ł�����B�E�ӂ͉^���ʖ��x�Ȃ̂ŁA�]���Ăs0�����s��0�ƂȂ�B
�@�@�E�@�s���� �� �s����
���̐}�ɉ����Ăs21�Ƃs12���l����B�s21�������̉��ɂx�����ɉ�]������͂ƂȂ�A�s12�������̉��ɂw�����ɉ�]������͂ƂȂ�B���������͉̂�]���Ă��Ȃ��̂łs21���s12�ł���B����Ĉ�ʂɁ@�s���� ���@�s�����@�ƂȂ�B
�@�@�@
�@�@�@

(2) �G�l���M�[�^���ʂ̕ۑ�
�s�͗��̂̂��G�l���M�[�Ɖ^���ʂ�\���Ă��邩��A�G�l���M�[��^���ʂ��ۑ������Ƃ������������Ȃ���Ȃ�Ȃ��B���̏����͂s�̔��U���O�Ƃ������ł���B
���L�̐}�ŗ��̒��̗��̗v�f������Ȓ����̂Ŏ������B�G�l���M�[�͑S�Ă̖ʂ�ʂ��ė����B�w�ʂ����闬��̊����� �[�s0�� �������� �� �[�s0���C�� ������������ �ƂȂ�B�i �[�s0���C�� �ɂ��Ă͉��L�������̋L�@���Q�� �j
�G�l���M�[�����o����̂ł��邩��l�͕��ł���B���l�ɂx�ʂ����闬��̊����� �[�s0�� �������� �� �[�s0���C�� ������������
�y�ʂ����闬��̊����� �[�s0�� �������� �� �[�s0���C�� ������������ �ƂȂ�B�����̊����̑��a�������̃G�l���M�[�̑����̊���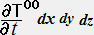 �� �s0���C�� ������������ �ł���B�]����
�� �s0���C�� ������������ �ł���B�]����
�@�@�@�s0���C�� �{ �s0���C�� �{ �s0���C�� �{ �s0���C�� �� �O�@�|�|�|���@�s0���C�� �� �O�@�i ����0�` 3 �j
�ƂȂ�A�G�l���M�[�ۑ��̖@�������藧�B
���L�̐}�̒��ŁA��ꓙ���̉E�ӂ̑�ꍀ�͔����̒�`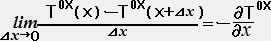 ��蓱�����B
��蓱�����B
�@�@�@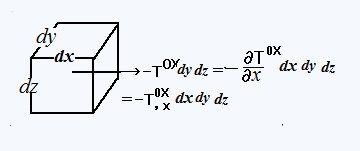
���l�ȕ��@�ʼn^���ʕۑ��̖@���@�si���C�� �� �O�@�����藧�B�@�@�i ����1�` 3 �j
��ʓI�ȕۑ����͂s�����C�� �� �O�ƂȂ�B
���̎��͓��ꑊ�Θ_�ł͑S�Ă̕����ɓK�p�o����B����̓e���\���̎l�������U�ł���B
�y�ʂ����闬��̊����� �[�s0�� �������� �� �[�s0���C�� ������������ �ƂȂ�B�����̊����̑��a�������̃G�l���M�[�̑����̊���
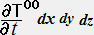 �� �s0���C�� ������������ �ł���B�]����
�� �s0���C�� ������������ �ł���B�]�����@�@�@�s0���C�� �{ �s0���C�� �{ �s0���C�� �{ �s0���C�� �� �O�@�|�|�|���@�s0���C�� �� �O�@�i ����0�` 3 �j
���L�̐}�̒��ŁA��ꓙ���̉E�ӂ̑�ꍀ�͔����̒�`
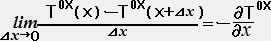 ��蓱�����B
��蓱�����B�@�@�@
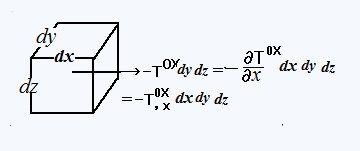
���l�ȕ��@�ʼn^���ʕۑ��̖@���@�si���C�� �� �O�@�����藧�B�@�@�i ����1�` 3 �j
��ʓI�ȕۑ����͂s�����C�� �� �O�ƂȂ�B
���̎��͓��ꑊ�Θ_�ł͑S�Ă̕����ɓK�p�o����B����̓e���\���̎l�������U�ł���B
�E�@������\���L�@�����̗l�ɒ�߂�B
�@�@�@�@�݃��^��X�����Cx�@�@�@�݃��^��X�������C�� �@�@�@��X���^��X����X���C��
�@�@�@�@�݃��^��X�����Cx�@�@�@�݃��^��X�������C�� �@�@�@��X���^��X����X���C��
(3) ���q���̕ۑ�
���̂��^�����Ă��鎞�ɑS���q�����ω����Ȃ��������蓾��B���̕ۑ�����(2)�Ɠ����l�ɓ������B����
�@�@�@�m���C�� �� �i���t���j�C�� �� �O �@�@�i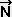 �� ��
�� �� �j
�j
�@�@�@�m���C�� �� �i���t���j�C�� �� �O �@�@�i
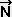 �� ��
�� �� �j
�j
�U�D���@�S�@���@��
���Θ_�ł̊��S���̂Ƃ͂l�b�q�n���S�����A�M�`�����Ȃ����̂̎��ł���B����̓_�X�g�ɂ��ň����̂��₳�������̂ł���B���̃X�g���X�[�G�l���M�[�e���\���͔��ɊȒP�Ȃ��̂ƂȂ�B
�E �M�`�����Ȃ���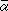
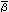 �͉��L�̂悤�ɂȂ�B
�͉��L�̂悤�ɂȂ�B
�@�@�@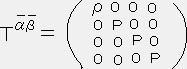
��̎�����ʍ��W�֕ϊ�����A��ʑ��ΐ����_�ł��p���鎖�̏o���銮�S���̂̃X�g���X�[�G�l���M�[�e���\����������B�n�Ɉˑ����Ȃ��`���͎��̂悤�ɂȂ�B
�@�@�s���� �� �i���{�o�j�t���t���{�o������
�@�@�y�ؖ��z �̐��� �i�P�C�O�C�O�C�O�j ���������Ƃ�������������̎��ɑ������ƁA�l�b�q�n�ł̃X�g���X�[�G�l���M�[�e���\��
�s
�̐��� �i�P�C�O�C�O�C�O�j ���������Ƃ�������������̎��ɑ������ƁA�l�b�q�n�ł̃X�g���X�[�G�l���M�[�e���\��
�s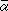
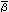 �����܂�B
�����܂�B
�E �M�`�����Ȃ���
�G�l���M�[�͗��q�̗���ɔ����Ă̂ݗ���邩��A�l�b�q�n�ł� �s0�� �� �s��0 �� �O �ł���B
�E �S�����Ȃ���
�S���̒�`���A���̗͂��Ȃ��Ƃ������͗͂͏�ɋ��E�ʂɐ����ł���B���� �� �� �� �Ȃ� �s���� �̓[���ł���B�ʂw�͂w�����̗݂͂̂��y�ڂ������A�ʂx�Ƃy�ɂ��Ă����l�ł���B�����̗͓͂��ʂȏ����͂Ȃ��̂œ������A�P�ʖʐς�����̗͈͂��͂o�ƌĂ��B
�ȏ�̎����犮�S���̂̂l�b�q�n�ł̃X�g���X�[�G�l���M�[�e���\�� �s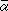
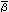 �͉��L�̂悤�ɂȂ�B
�͉��L�̂悤�ɂȂ�B�@�@�@

��̎�����ʍ��W�֕ϊ�����A��ʑ��ΐ����_�ł��p���鎖�̏o���銮�S���̂̃X�g���X�[�G�l���M�[�e���\����������B�n�Ɉˑ����Ȃ��`���͎��̂悤�ɂȂ�B
�@�@�s���� �� �i���{�o�j�t���t���{�o������
�@�@�y�ؖ��z
�l�b�q�n�i ���s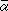
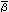 �j
�����ʂ̍��W�n�i ���s���� �j�ւ̃��[�����c�ϊ����s���B����
�j
�����ʂ̍��W�n�i ���s���� �j�ւ̃��[�����c�ϊ����s���B����
�@�@�@�s���� ��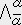
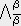 �s
�s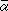
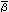
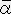 ��
�� 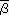 �Ȃ� �s
�Ȃ� �s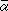
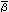 �� �O ������
�� �O ������
�@�@�@�s���� �� ��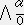
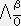 �{ �o
�{ �o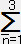
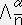
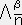 �@�@�@�E�E�E�E�E�@�i�P�j
�@�@�@�E�E�E�E�E�@�i�P�j
��������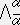
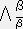 ��
��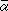
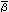 �@�C�@��
�@�C�@��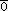
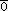 ���|�P
�@�C�@��
���|�P
�@�C�@��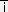
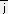 ����
����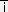
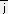 �@������@�@�i���̓N���l�b�J�[�̃f���^)
�@������@�@�i���̓N���l�b�J�[�̃f���^)
�@�@�@���������[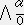
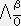 �{
�{ 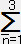
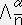
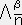 �@�@�@�@�@�E�E�E�E�E�@�i�Q�j
�@�@�@�@�@�E�E�E�E�E�@�i�Q�j
�i�P�j�|�i�Q�j���o���v�Z�����
�@�@�@�s�����[�o������ ��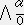
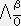 �i���{�o�j
�i���{�o�j
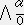 ��
�� 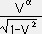 �� �t���@�C�@
�� �t���@�C�@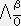 ��
�� 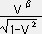 �� �t��
������
�� �t��
������
�̂Ɂ@�s���� �� �i���{�o�j�t���t���{�o������
�l�b�q�n�ł� 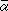
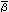 �j
�����ʂ̍��W�n�i ���s���� �j�ւ̃��[�����c�ϊ����s���B����
�j
�����ʂ̍��W�n�i ���s���� �j�ւ̃��[�����c�ϊ����s���B�����@�@�@�s���� ��
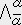
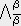 �s
�s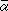
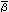
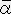 ��
�� 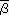 �Ȃ� �s
�Ȃ� �s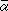
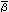 �� �O ������
�� �O �������@�@�@�s���� �� ��
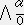
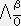 �{ �o
�{ �o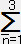
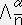
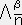 �@�@�@�E�E�E�E�E�@�i�P�j
�@�@�@�E�E�E�E�E�@�i�P�j��������
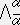
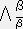 ��
��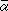
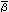 �@�C�@��
�@�C�@��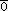
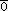 ���|�P
�@�C�@��
���|�P
�@�C�@��
 ����
����
 �@������@�@�i���̓N���l�b�J�[�̃f���^)
�@������@�@�i���̓N���l�b�J�[�̃f���^)
�@�@�@���������[
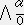
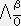 �{
�{ 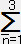
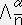
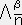 �@�@�@�@�@�E�E�E�E�E�@�i�Q�j
�@�@�@�@�@�E�E�E�E�E�@�i�Q�j�i�P�j�|�i�Q�j���o���v�Z�����
�@�@�@�s�����[�o������ ��
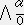
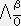 �i���{�o�j
�i���{�o�j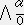 ��
�� 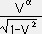 �� �t���@�C�@
�� �t���@�C�@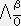 ��
�� 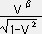 �� �t��
������
�� �t��
�������̂Ɂ@�s���� �� �i���{�o�j�t���t���{�o������
 �̐��� �i�P�C�O�C�O�C�O�j ���������Ƃ�������������̎��ɑ������ƁA�l�b�q�n�ł̃X�g���X�[�G�l���M�[�e���\��
�s
�̐��� �i�P�C�O�C�O�C�O�j ���������Ƃ�������������̎��ɑ������ƁA�l�b�q�n�ł̃X�g���X�[�G�l���M�[�e���\��
�s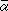
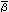 �����܂�B
�����܂�B
�V�D�K�E�X�̔��U�̒藝
�O�����̃x�N�g����͂ŃK�E�X�̔��U�̒藝�Ƃ����藝������B���̒藝���l�����̏ꍇ�ɂ����藧���������B�K�E�X�̔��U�̒藝�͎��̗l�Ȃ��̂ł���B
�@�@�@ ��
��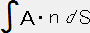 �@�|�|�|�|�|���@
�@�|�|�|�|�|���@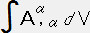 ��
��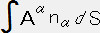 �@�E�E�E�E�E�E�@�i�P�j
�@�E�E�E�E�E�E�@�i�P�j
���ӂ̓x�N�g����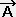 �̔��U�̑̐ϐϕ��ŁA�E�ӂ̓x�N�g��
�̔��U�̑̐ϐϕ��ŁA�E�ӂ̓x�N�g��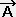 ���P�ʐ�����`���̓��ς̕\�ʐϕ��ł���B���̈Ӗ��́A�x�N�g����̔��U�̑̐ϐϕ��ƕ\�ʐϕ��͓������B���̓x�N�g����̔��U�̑̐ϐϕ���\�ʐϕ��ɒ������ł���B�x�N�g����̔��U�Ƃ̓x�N�g����̒P�ʑ̐ς̕ω��̊����ŃX�J���[�ȗʂŁA���̗l�ȗʂł���B
���P�ʐ�����`���̓��ς̕\�ʐϕ��ł���B���̈Ӗ��́A�x�N�g����̔��U�̑̐ϐϕ��ƕ\�ʐϕ��͓������B���̓x�N�g����̔��U�̑̐ϐϕ���\�ʐϕ��ɒ������ł���B�x�N�g����̔��U�Ƃ̓x�N�g����̒P�ʑ̐ς̕ω��̊����ŃX�J���[�ȗʂŁA���̗l�ȗʂł���B
�@�@�@������ �`���݂`t�^�����{�݂`x�^�݂w�{�݂`y�^�݂x�{�݂`z�^�݂y
�i�P�j�̍��ӂ�
�@�@�@�� �i�݂`t�^�����{�݂`x�^�݂w�{�݂` y�^�݂x�{�݂`z�^�݂y�j���u
�i�P�j�̉E�ӂ̈Ӗ��������ׂ����ʂɉ�����\�ʐϕ���`�����B
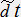 �ł���B���̐����́i�P�C�O�C�O�C�O�j�ł���B���P�ʂɉ�����P�ʐ�����`���́[
�ł���B���̐����́i�P�C�O�C�O�C�O�j�ł���B���P�ʂɉ�����P�ʐ�����`���́[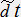 �ł���B���̐����́i�[�P�C�O�C�O�C�O�j�ł���B�]�������ʂɉ�����\�ʐϕ���
�ł���B���̐����́i�[�P�C�O�C�O�C�O�j�ł���B�]�������ʂɉ�����\�ʐϕ���
�@�@�@�� �i�`t�i���Q�j�[�`t�i���P�j�j�������������@�E�E�E�E�E�E�@�i�Q�j
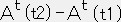 ��
�� 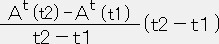 �@�C�@
�@�C�@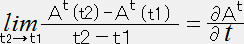 �@�@������
�@�@������
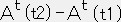 ��
�� 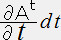 �@�ƂȂ�B���̎����i�Q�j�ɑ������Ɓi�Q�j��
�@�ƂȂ�B���̎����i�Q�j�ɑ������Ɓi�Q�j��
�@�@�@�� �i�݂`t�^�����j���������������� ���� �i�݂`t�^�����j���u
���l�ɂw�ʂɉ�����\�ʐϕ��� �� �i�݂`x�^�݂w�j���u�@�C�@�x�ʂɉ�����\�ʐϕ��� �� �i�݂`y�^�݂x�j���u
�y�ʂɉ�����\�ʐϕ��� �� �i�݂`�y�^�݂y�j���u
����āi�P�j�̉E�ӂ�
�@�@�@�� �i�݂`t�^�����{�݂`x�^�݂w�{�݂` y�^�݂x�{�݂`z�^�݂y�j���u
����́i�P�j�̍��ӂƑS�������ł���B
�@�@�@���@�K�E�X�̔��U�̒藝�͎l�����̏ꍇ�ɂ����藧�B
�@�@�@
 ��
��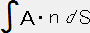 �@�|�|�|�|�|���@
�@�|�|�|�|�|���@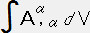 ��
��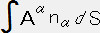 �@�E�E�E�E�E�E�@�i�P�j
�@�E�E�E�E�E�E�@�i�P�j���ӂ̓x�N�g����
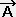 �̔��U�̑̐ϐϕ��ŁA�E�ӂ̓x�N�g��
�̔��U�̑̐ϐϕ��ŁA�E�ӂ̓x�N�g��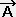 ���P�ʐ�����`���̓��ς̕\�ʐϕ��ł���B���̈Ӗ��́A�x�N�g����̔��U�̑̐ϐϕ��ƕ\�ʐϕ��͓������B���̓x�N�g����̔��U�̑̐ϐϕ���\�ʐϕ��ɒ������ł���B�x�N�g����̔��U�Ƃ̓x�N�g����̒P�ʑ̐ς̕ω��̊����ŃX�J���[�ȗʂŁA���̗l�ȗʂł���B
���P�ʐ�����`���̓��ς̕\�ʐϕ��ł���B���̈Ӗ��́A�x�N�g����̔��U�̑̐ϐϕ��ƕ\�ʐϕ��͓������B���̓x�N�g����̔��U�̑̐ϐϕ���\�ʐϕ��ɒ������ł���B�x�N�g����̔��U�Ƃ̓x�N�g����̒P�ʑ̐ς̕ω��̊����ŃX�J���[�ȗʂŁA���̗l�ȗʂł���B�@�@�@������ �`���݂`t�^�����{�݂`x�^�݂w�{�݂`y�^�݂x�{�݂`z�^�݂y
�i�P�j�̍��ӂ�
�@�@�@�� �i�݂`t�^�����{�݂`x�^�݂w�{�݂` y�^�݂x�{�݂`z�^�݂y�j���u
�i�P�j�̉E�ӂ̈Ӗ��������ׂ����ʂɉ�����\�ʐϕ���`�����B
�@�@�@�@�@�@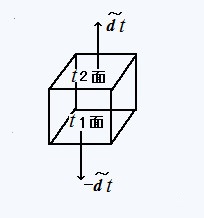
���Q�ʂɉ�����P�ʐ�����`����
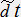 �ł���B���̐����́i�P�C�O�C�O�C�O�j�ł���B���P�ʂɉ�����P�ʐ�����`���́[
�ł���B���̐����́i�P�C�O�C�O�C�O�j�ł���B���P�ʂɉ�����P�ʐ�����`���́[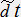 �ł���B���̐����́i�[�P�C�O�C�O�C�O�j�ł���B�]�������ʂɉ�����\�ʐϕ���
�ł���B���̐����́i�[�P�C�O�C�O�C�O�j�ł���B�]�������ʂɉ�����\�ʐϕ����@�@�@�� �i�`t�i���Q�j�[�`t�i���P�j�j�������������@�E�E�E�E�E�E�@�i�Q�j
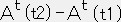 ��
�� 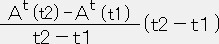 �@�C�@
�@�C�@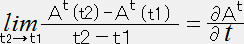 �@�@������
�@�@������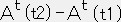 ��
�� 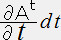 �@�ƂȂ�B���̎����i�Q�j�ɑ������Ɓi�Q�j��
�@�ƂȂ�B���̎����i�Q�j�ɑ������Ɓi�Q�j���@�@�@�� �i�݂`t�^�����j���������������� ���� �i�݂`t�^�����j���u
���l�ɂw�ʂɉ�����\�ʐϕ��� �� �i�݂`x�^�݂w�j���u�@�C�@�x�ʂɉ�����\�ʐϕ��� �� �i�݂`y�^�݂x�j���u
�y�ʂɉ�����\�ʐϕ��� �� �i�݂`�y�^�݂y�j���u
����āi�P�j�̉E�ӂ�
�@�@�@�� �i�݂`t�^�����{�݂`x�^�݂w�{�݂` y�^�݂x�{�݂`z�^�݂y�j���u
����́i�P�j�̍��ӂƑS�������ł���B
�@�@�@���@�K�E�X�̔��U�̒藝�͎l�����̏ꍇ�ɂ����藧�B