|
|
| ___ |
目次 【 概要 】 二重スリット実験 玉突きモデル 二つの条件 真空と経路積分 波と粒子と区別の問題 二つの数学空間 数学的空間の切り替え 途中観測の場合 |
二重スリットの問題は、量子力学の観測問題として理解される。これに対する回答としては、コペンハーゲン解釈およびエヴェレット解釈がある。しかし、いずれの解釈にも、難点がある。そこで、新たな解釈を示す。この解釈を「二重空間モデル」もしくは「二重空間モデル解釈」と称する。(「南堂解釈」と称してもよい。通称で。)
二重空間モデルでは、量子は「粒子」または「波」のどちらか一方で理解されるかわりに、二通りで理解される。次のように。
・ 計算されたもの …… 波
・ 観測されたもの …… 粒子
たとえば、二重スリットの実験がある。電子を発射したあと、二本のスリットを経由して、感光板に達する。ここでは、量子力学で計算された状態(未観測状態)では、量子は「波」である。しかるに、到着点では、観測されているので、量子は「粒子」である。
つまり、観測というのは、(考察対象としての)量子を、「波」から「粒子」に転じることなのだ。こう理解すると、さまざまな難点が解決する。
たとえば、電子を一つずつ発射しても、干渉が起こるが、それというのも、計算された量子は「波」であるからだ。一つの粒子を発射したあと、一つの粒子が二つのスリットを通り抜けたのではなくて、波が二つのスリットを通り抜けただけだ。また、到着点で観測すると、波動関数が急激に収束したように見えるが、実は、計算された波動関数が急速に収束したのではなくて、考察対象が、波動関数で計算される「波」の世界から、「粒子」の世界へと転じただけだ。
ここでは、「波」の世界と「粒子」の世界とが、二重に存在することになる。正確に言えば、現実の世界は一つだが、それに対応する数学的世界が二つあることになる。そして、現実の世界と数学的世界との対応関係が、人間が認識したときに切り替えられることになる。
「波」 の 世界
現実世界(1つ) < ↓ 観測
「粒子」の世界
このような切り替えは、別に、不自然なことではない。確率では一般に見られることだ。たとえば、コインをトスして、蓋で伏せる。その時点では、裏表は50%の確率だ。そのまま、1年経過する。1年後に、蓋をはずして、コインを観測する。その時点で、裏か表かが判明する。──ここでは、1年後に、「確率が50%から、0%または100%に変動する」という現象が起こったわけではない。確率は、最初から最後までずっと50%のままだ。ただし、確率とは別の世界で、コインの裏表が判明しただけだ。
確率の世界とは、裏の確率が0%から100%までの中間値があるような、実数の世界(連続的な世界)だ。現実のコインの世界とは、裏か表かのどちらかだけがあるような、自然数の世界(離散的な世界)だ。この二つは、別々の数学空間を形成する。そして、観測したときに、一方から他方へと移行する。
確率の場合には、そういうふうに二重の数学空間が成立する。それと同様に、量子力学の場合も、二重の数学空間が成立する。そして、観測とは、一方の数学空間から、他方の数学空間へと、切り替えることである。それは決して、一つの数学空間のなかで、数値が急激に収束することではない。
以上が「二重空間モデル」のあらましだ。
二重空間モデルでは、波動関数は、「粒子」としての量子の「存在確率」を示すのではない。計算された量子はもともと「波」なのだから、それを「粒子」とみなして「粒子」の「存在確率」を考えても、無意味である。
二重空間モデルで理解すると、二重スリットの問題や、シュレーディンガーの猫の問題が、ごく自然に理解される。そしてまた、ファインマンの経路積分や、場の量子論も、ごく自然に理解される。
本論では、二重スリット実験を取り上げる。これは、たまたま興味深いからではなくて、ここには量子力学の核心があるからだ。たとえば、ファインマンは、この実験を評して、「量子力学の神髄だ」と言った。
では、二重スリット実験とは、どんなものか? 量子力学の教科書には、たいてい書いてあるので、研究者ならば誰でも知っているはずだ。一応、簡単に示せば、次の通り。
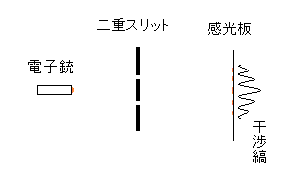
電子銃から電子を発射して、二本のスリットを通過させると、その先の感光板(写真乾板)で、干渉縞が発生する。これは電子が波の性質をもつことを示唆する。

|
さて。複数の電子を同時に発射するのであれば、複数の電子が相互に干渉することもあるだろう。では、電子を一つずつ発射したときは、どうか?
この場合、電子は一つだけなのだから、干渉するはずがない。干渉するにも、干渉する相手がないからだ。ところが、現実には、干渉が起こる。つまり、電子を一つずつ発射しても、それらの電子をたくさん蓄積すると、感光板には同じような干渉縞が現れる。このことは、ホログラフィ電子顕微鏡の研究者によって、実験的に示された。( → 外村彰 [1989年])
さて。実験事実はわかったが、これについての解釈が問題となる。通常は、次のように解釈される。
「一つずつ電子が発射されても干渉縞が生じるのは、電子が二つのスリットを同時に通過したからだ」
しかし、これは、あまりにも不自然である。「一つの粒子が二つのスリットを通る」なんてのは、ほとんど言語矛盾だ。「半分ずつ通る」ならばまだわかるが、「半分ずつ通る」というわけではない。
( ※ 言語矛盾だけでなく、物理学的な矛盾もある。「一つの粒子が二つのスリットを通る」というのは、「一つの粒子が同時に別の場所に存在する」ということであるから、相対論に矛盾する、とすら言える。時間差ゼロで別の場所に移動しているのと同じことだからだ。)
これは問題だ。そこで、次のような解釈が出た。(「コペンハーゲン解釈」と呼ばれる。)
「電子が発射されたあとでは、電子の存在確率が、波動関数で示される。途中で二重スリットを通り抜ける時点でも、電子は波動関数で示されるので、存在確率が雲のように拡散しながら、二重スリットを通り抜ける。その後、波動関数が感光板に達すると、観測される。観測された時点で、波動関数が急激に収束して、電子は一点に決定される」
この発想では、電子がスリットを通り抜けるのではなくて、電子の存在確率のようなものがスリットを通り抜けるだけだ。というわけで、「一つの粒子が二つの場所を通る」という言語矛盾は避けられる。しかし、そのかわり、物理学としての矛盾が発生する。それは、次の三点だ。
(i) 意識の作用
この主張では、人間の観測による意識が、現実を決定することになる。人間が観測することで、波動関数が急激に収束する。とすれば、人間が観測していない限りは、波動関数は収束していないことになる。……つまり、感光板の感光状態は、人間が観測するまでは曖昧であり、人間が観測したとたんに感光状態が決まることになる。これでは、あまりにも不自然だ。
(ii) 感光板の感光機能の違い
観測というのが、人間なしに客観的に生じる(たとえば機械的または化学的に感光板の状態が確定する)としたら、それはそれで、おかしな結論が生じる。つまり、「感光板では波動関数が収束するが、感光板の感光機能がなければ、波動関数が収束しない」という結論が出る。たとえば、感光板の位置に、ただの壁面を立てておけば、何も観測されないので、波動関数も収束しない。
もっと極端に言えば、感光板として、電子計数管を用いよう。電子計数管のスイッチをOFFにしておけば、電子計数管はただの壁であるから、波動関数は収束しない。電子計数管のスイッチをONにすると、波動関数が収束する。電子計数管のスイッチが波動関数の状態を決めることになる。これは、「人間の意識が決める」というかわりに、「機械的なON・OFFが決める」というふうになるが、やはり、不自然である。
(iii) 相対論パラドックス
少し前の (i) において、時間を導入しよう。電子を発射した時点から、電子が到着した時点までは、ほぼ一瞬である。感光した時点も、ほぼ同時点である。それは6月のことであったとする。そのまま、人間が観測しないでいたとする。その後、2カ月たって、8月になってから、観測したとする。すると、観測が状態を決定するのであるから、観測した時点である8月に、感光状態は決定したことになる。ところが、現実に感光したのは6月である。6月から8月までの2カ月の間、感光状態が未確定であった。ところが、8月に観測すると、それまでの2カ月の状態が確定した。つまり、8月の観測結果が、6月の時点にさかのぼって、6月の状態を決定したわけだ。つまり、8月の情報が、6月という過去に流れ込んだことになる。その後、6月から8月までの2カ月間の歴史は、「未確定」から「確定」に転じてしまったことになる。つまり、未来の情報が過去に流れ込んだせいで、2カ月間の歴史が書き換えられてしまったことになる。──これは、相対論に矛盾する。
コペンハーゲン解釈には、上記の難点がある。そこで、新たな解釈が出た。それは「並行宇宙がある」と主張して、いろいろと説明する解釈だ。これは「エヴェレット解釈」と呼ばれる。
エヴェレット解釈には、コペンハーゲン解釈のような矛盾は生じない。というのも、矛盾を示そうにも、しょせんはどこか他の宇宙のことなのであるから、どうにも説明のしようがないのだ。
エヴェレット解釈の「並行宇宙がある」という主張は、いわば、狂人の妄想である。狂人にはそれがまともだと信じられるのだろうが、しょせん、狂人の妄想であるから、いちいち「間違っている」と証明することはできない。そして狂人は、「おれの妄想が間違っていると証明できる人はいないから、おれの妄想は真実なのだ」というふうに主張する。
それはそうかもしれないが、間違っていると証明できないからといって、正しいということにはならない。こんな狂気的な発想を相手にする方が馬鹿げているだろう。(ちなみに言えば、こんな発想を信じているのは、量子論学者だけである。だから量子論学者は馬鹿にされるのだが。……なお、量子論学者のQ氏が「自分は正しい」と主張しても、別の宇宙では、同じQ氏が「自分は間違っている」と主張しているはずだ。ゆえに、あなたがエヴェレット解釈を「正しい」と信じても、ほとんど無意味である。この世界ではあなたは狂人かもしれないが、別の世界ではあなたは正気かもしれない。)
ともあれ、以上のようにして、コペンハーゲン解釈にも、エヴェレット解釈にも、難点があることがわかった。この難点は、「観測問題」という形で、「シュレーディンガーの猫」という問題にも、同様に適用される。
結局、どちらの解釈を取るにせよ、とうてい万人を納得させるような説明とはならない。その意味で、現在の量子力学は、「それが何を意味するか」という点で、あまりはっきりとしたことはわかっていないのである。たしかに数式によっていろいろと結果は出るのだが、その数式が本質的には何を意味しているかは、はっきりとしないのだ。
その典型が、二重スリットの実験である。量子力学の数式を使えば、「このような観測結果が出る」ということは、見事に説明される。その意味で、量子力学は正しい。とはいえ、「どうしてそういう結果が出るか」ということは、さっぱりわかっていないのだ。今の量子力学では、二重スリットの実験でも、出発点と到着点のことがわかっているだけであり、その途中過程はすっぽりとブラックボックスに入っているのも同然である。
工学技術者ならば、「最後の実験結果さえわかれば、それでいい」と思うだろうが、真実を探る科学者ならば、「世界の真実を解き明かしたい」と思うだろう。そして、その望みに対して、現在の量子力学は、ほとんど矛盾した説明しか提出してくれないのである。──その意味で、現在の量子力学は、本質的には未完成なのだ。
ここで、新たなモデルを提出する。このモデルを「玉突きモデル」と称する。
玉突きモデルでは、量子は「粒子」または「波」のどちらか一方で理解されるかわりに、二通りで理解される。次のように。
・ 計算されたもの …… 波
・ 観測されたもの …… 粒子
たとえば、二重スリットの実験がある。電子を発射したあと、二本のスリットを経由して、感光板に達する。ここでは、量子力学で計算された状態(未観測状態)では、量子は「波」である。しかるに、到着点では、観測されているので、量子は「粒子」である。
ここで、観測された量子が「粒子」である、ということは、特に説明が不用だろう。現実に観測されているわけだから、「粒子」と見なしていいはずだ。(「波」として見てもいいが、その場合、鋭いピークをもつのだから、実質的には、「粒子」として見るのと同様だ。)
問題は、観測されていない状態だ。なぜ、この状態の量子は、「波」と見なされるのか? それは、以下の理由だ。

これは、パチンコ玉かガラス玉を当てた図だ、と解釈してよい。
左から ◯ を発射すると、たくさんある ◯ の列にぶつかり、その後、列の反対側から、別の ◯ が飛び出す。ここでは、発射した ◯ と、飛び出した ◯ とは、別のものだ。しかしながら、観測者は、こう考える。
「出発点では、 ◯ が発射されて、到達点では、 ◯ が出現した。どちらも同じ粒子だ。とすれば、一つの粒子が、出発点から到達点に移動したはずだ」
実は、これは、一種のトリックである。似たような事例は、他にも挙げられる。
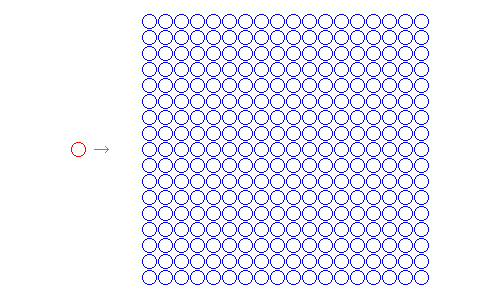
左端の ◯ が、たくさんある ◯ の集団にぶつかる。すると、その衝撃は、 ◯ の集団の全体に、平面上の波として伝わるだろう。つまり、最初にぶつかった一点を中心として、弧を描くようにして、平面全体に伝わるだろう。
これがつまり、「波として伝わる」ということだ。
( ※ 数学的に言えば、「ソリトン」として考えるといい。当然、「場の量子論」や「固体物理学」などとも関連する。アナロジー関係があることは、専門家ならばわかるだろう。)
さて。このことは、二重スリットに適用可能だろうか? 適用可能であるためには、次の二件が必要不可欠だ。
(1) 「真空」と呼ばれる空間には、量子が充満していること。
(2) 量子はたがいに区別不可能であること。
この二件について説明しよう。
(1) の件は、今日の量子論では、かなり受け入れられている。真空は、素人が想像するように「何もない空間」ではなくて、量子が充満しているのだ。──ただし、量子が充満しているというのは、先の ◯ のモデルとはいくらか異なる。真空状態では、 ◯ が密集するように、電子が密集しているのではない。かわりに、電子と反電子が密集しているのだ。たとえば、電子が真空にぶつかると、 ◯ としての電子と電子とがぶつかりあう形で波が伝播するのではなくて、電子と反電子とが消滅・発生を繰り返しながら伝播していくのだ。──この「消滅・発生」という発想は、「場の量子論」と呼ばれる発想である。ともあれ、(1) の件は、従来の量子論では受け入れられている内容だ、とわかる。
(2) の件も、従来の量子論では受け入れられている。「ボース粒子」「フェルミ粒子」などの語で称される。
以上をまとめて言えば、こうだ。
電子銃から電子を発射すると、感光板で電子が感光する。それを見て、「電子が移動した」と物理学者は考える。ここでは、「電子は粒子だ」ということが前提されている。その前提のもとで、「電子が移動した」と判断して、さらに、「電子はどこかを通ったが、そのどこかとは、二本のスリットだ」と考える。そして、「二本のスリットの一方だけを通ったと仮定すると、矛盾が生じるから、二本のスリットの両方を通ったはずだ」 と結論する。
その論理では、「一方のスリットを通った」と考えると矛盾するから、二本のスリットを通ったはずだ」というふうになる。しかし、「二本のスリットを通った」と仮定しても、先の (iii) の「相対論パラドックス」という矛盾が生じるのだ。
だから、間違っているのは、「一方のスリットを通った」ということ(だけ)ではなくて、「粒子が通った」ということなのだ。本当は、一つの粒子が次々と移動していったのではなくて、波が伝播しただけなのだ。
(1) の件(真空に量子が満ちていること)について、さらに言及しよう。
まず、「真空とは何か」について考えよう。
前述のように、「真空は何もない空間ではない」と言える。これは、「真空は透明だ」と表現してもよい。地上の空間は光が素通りするので、あたかも何も存在しないように見えるが、実際は、空気( air )が存在する。なのに空気が観測されないのは、空気が透明であるからだ。真空もまた、同様である。地上には空気が満ちているように、宇宙には真空が満ちているのだが、そこを光子や電子が素通りするから、何もないように感じられるだけだ。
なお、「宇宙空間は透明だ」ということの証拠はある。それは、「透明な物体の屈折率が変わると、光がレンズで屈折する」ように、「宇宙空間に重力が働くと、光が重力レンズで屈折する」ということだ。
( ※ このことからわかるように、相対論というのは、宇宙空間についての幾何学である。相対論と量子論とは、密接に関連する。両者の関係は、「媒体と波」という関係だ。)
( ※ 念のために補足しておくと、「絶対静止空間」としての「エーテル ( ether )」というものを想定しているわけではない。エーテルは真空の上に載っかる形で存在するものだが、本論で述べているのは真空そのものだ。)
さて。「真空は何もない空間ではない」と見なすと、「真空には波が伝播する」という発想が可能だ。そこで、本論の解釈では、こう考える。
「電子銃から電子が発射されたとき、粒子が何もないところを通ったのではなくて、波が真空を伝播した」
こう考えることには、非常に大きなメリットがある。それは、ファインマンの経路積分の発想が適用できる、ということだ。
ファインマンの経路積分というのは、二重スリットで言えば、「二つの経路だけを考える」のでははなくて、「あらゆる複雑な経路をすべて考慮して、その平均値を取る」ということに相当する。たとえば、
電子銃 → 二つの穴 → 感光板
という最短経路のほか、途中で行ったり来たりして、寄り道したりして、あっちへ行ってからまた戻ってくる、というような、複雑な経路をすべて考慮する。そして、それはまさしく、波の伝播と同様なのだ。(詳しい説明は省くが、水面波の波紋がどのようにして決まるかを理解している人ならば、すぐにわかるだろう。)
さて。ファインマンの経路積分は、「波」の伝播を記述するのにほぼ相当する。実際、ファインマンの方法を見ると、そこにはまさしく「波」として扱う発想がある、とわかる。(たとえば、位相の重なり合いなどを考慮する。)
では、ファインマンの経路積分を使うと、どんなメリットがあるか? それは、量子力学を知っている人であれば、よく理解しているとおりだ。すなわち、数式の計算結果は、従来の量子力学の計算結果とまったく変わらない。ただし、計算過程が、ごく簡単になるのだ。
そして、数学の歴史は、次のことを経験的に教える。
「まったく同じ結果をもたらすような、二つのまったく異なる発想法や数式があるならば、簡単な方は物事の真実をつかんでおり、複雑な方は物事の真実をつかみそこねている」
二重スリットの実験に即して言えば、こうなる。
「ファインマンの経路積分は、計算された量子が波であるということをまさしく示しているので、直接的な記述となり、簡単になる。従来の量子論は、計算された量子を粒子の存在確率を示すものとして示しているので、もってまわった記述になり、複雑になる」
要するに、計算された量子を「粒子」と考えて、移動中の存在確率をあれこれと計算するよりは、計算された量子を「波」と考えて、伝播の仕方を考える方が、ずっとシンプルに済む、ということだ。そして、シンプルに済むということは、それだけ真実をよくとらえているということになる。
(2) の件(量子はたがいに区別不可能であること)について、さらに言及しよう。
先の ◯ のモデルでは、玉突き現象が起こっている、と考えた。特に、一列の
◯◯◯◯◯◯◯
というモデルでは、次々と玉突きが起こっている、と考えた。ここでは、ぶつかった ◯ と、ぶつかられた ◯ とは、別々である。
ただし本当は、この ◯ と ◯ は、たがいに区別がつかない。どっちが「ぶつかったもの」「ぶつけられたもの」であるか、区別がつかない。一つの ◯ がどんどん進行しているように見えるとき、本当に一つの ◯ がどんどん進行しているのか、あるいは ◯ が玉突き現象をしているだけなのか、区別がつかない。なぜなら、 ◯ と ◯ とは、たがいに区別がつかないからだ。
だから、「 ◯ と ◯ とが区別がつかない」ということは、「一つの ◯ がどんどん進行していることと、 ◯ の玉突き現象が起こっていることとが、区別がつかない」ということだ。
だから、現実には、 ◯ と ◯ とがぶつかったあとで、一つの ◯ がどんどん進行しているのかもしれない。しかし、だとしても、そのとき ◯ はぶつかって振動しながら移動しているのであるから、玉突き現象が起こっているのと同然であり、それゆえ、「玉突き現象が起こっている」と判定しても構わないのだ。──それが本論の立場だ。
つまり、 ◯ のモデルは、「玉突き現象で一つの ◯ が移動することは、決してない」と主張しているわけではない。
( ※ ただし現実には、一つの ◯ が長距離を移動する確率は、限りなく小さいだろう。一方、一つの ◯ が粒子二つ分ぐらいの距離を移動する確率は、少しはあるだろう。……あくまで、確率の問題となる。計算するなら、区別できない二つのものから一つを得る確率は 50%だから、衝突が1回起こるたびに、同一粒子である確率は半分になる。回数が増えるにつれて、同一粒子である確率は、指数関数的に減少していく。)
( ※ なお、同一であろうとなかろうと、それを判定する方法はないだろう。同じDNAをもつ双生児をうまく区別できないのと同然だ。本人には違いがわかるのだろうが、他人には違いがわからない。)
波と粒子と観測の問題について考えよう。
真空中を伝わるものは、計算された量子であり、「波」である。それは目に見えない。ただし、観測された時点で、目に見えるようになる。では、観測とは、何なのか?
コペンハーゲン解釈では、観測とは、「波動関数が収束すること」であった。ここでは、「観測という人間の行為が、物質レベルの波動関数を収束させる」ということになった。しかし、それは、あまりにも不自然である。また、先の「相対論パラドックス」という矛盾を引き起こす。では、正しくは?
本論の発想では、計算された量子は「波」であり、一方、観測された電子は「粒子」である。つまり、観測したことによって、考察対象が「波」から「粒子」に転じる。では、それは、何を意味するか?
量子そのものが「波」から「粒子」に転じるのではない。考察対象が「波」から「粒子」に転じるだけだ。それはあくまで、考察における出来事であるから、現実世界を左右したりはしない。
コペンハーゲン解釈では、現実世界における波動関数が急激に収束したことになる。一方、二重空間モデルでは、波動関数は最初から最後までずっと同様である。たとえば、ずっと50%のままだ。それは空想的な理論世界に属する。一方、観測されたものは、波動関数で示されるものではなくて、現実に目で判定されるものだ。それは理論に依存することはない。
もう少しわかりやすく言おう。コペンハーゲン解釈を信じる研究者ならば、自分が観測したとき、それまでの計算数値と比較して、「波動関数が急激に収束した」と主張するだろう。一方、ただの子供が観測したならば、「波動関数が急激に収束した」なんて主張することはなく、「観測結果はこれこれだったよ」と描写するだろう。ここでは、波動関数が子供の頭のなかで、急激に出現したのではない。波動関数なんてものは、最初から最後まで、子供の頭には出現しなかったのだ。出現したのは、波動関数とは何の関係もない、ただの観測結果であるにすぎない。
結局、現実の世界は一通りだが、対応する数学空間は二通りあるわけだ。次のように。
理論 の世界
現実世界(1つ) < ↓ 観測
現実 の世界
観測は、理論の世界で急激な変動を引き起こすのではなくて、理論の世界から現実の世界へと、数学的空間を切り替えることに相当する。ここでは、理論というものはまったく成立していなくてもいい。(たとえば、子供の場合。)あるいは、理論というものがまったく間違った理論であってもいい。(たとえば、古典力学にもとづく量子論。)……いずれにせよ、理論の世界が何であれ、それにかかわらず、観測したときに現実の結果が判明する。
そして、このことは、特に本論でいえば、次のことに相当する。
「波」 の 世界
現実世界(1つ) < ↓ 観測
「粒子」の世界
理論の世界は、「波」の世界である。現実の世界は、「粒子」の世界である。観測という人間の行為は、この二つの世界を切り替える。
そして、この二つの世界というのは、現実ではなくて、認識法としての世界だ。それは数学的空間に相当する。
つまり、「一つの現実世界に、二つの数学的空間が対応しておいて、その二つの数学的空間を切り替えるのが、観測だ」と言える。──これが、本論の立場だ。
「数学的空間の切り替え」というのは、あまりにご都合主義に思えるかもしれない。しかし、そんなことはない。このような切り替えは、量子論に限らず、しばしば見られることだ。特に、確率ではそうだ。
たとえば、コインをトスして、蓋で伏せる。その時点では、裏表は50%の確率だ。そのまま、1年経過する。1年後に、蓋をはずして、コインを観測する。その時点で、裏か表かが判明する。──ここでは、1年後に、「確率が50%から、0%または100%に変動する」という現象が起こったわけではない。確率は、最初から最後までずっと50%のままだ。ただし、確率とは別の世界で、コインの裏表が判明しただけだ。
( ※ なお、「蓋をした時点で、確率が変動した」と仮定すると、1年後に観測したことによって、過去の時点の確率が決定されたことになる。未来が過去を決定したことになる。これは相対論に矛盾する。……前述の相対論パラドックス。)
確率の世界とは、裏の確率が0%から100%までの中間値があるような、実数の世界(連続的な世界)だ。現実のコインの世界とは、裏か表かのどちらかだけがあるような、自然数の世界(離散的な世界)だ。この二つは、別々の数学空間を形成する。そして、観測したときに、一方から他方へと移行する。
確率の場合には、そういうふうに二重の数学空間が成立する。それと同様に、量子力学の場合も、二重の数学空間が成立する。そして、観測とは、一方の数学空間から、他方の数学空間へと、切り替えることである。それは決して、「一つの数学空間のなかで、数値が急激に収束すること」ではない。
さて。問題は、この二つの数学空間とはどのようなものか、ということだ。実は、これは、数学において考察されるべきことであり、かなり難解となる。ゆえに、ここでは、細かなことは説明しないでおく。
ただし、核心を示せば、次の二つの数学空間だ。
・ 個々の要素がたがいに区別不可能である空間
・ 個々の要素がたがいに区別可能である空間
こう分けると、次のような分け方が成立する。
・ 量子は、たがいに区別不可能である
・ 現実世界の物体は、たがいに区別可能である
たとえば、個々の自動車や電器製品は、たとえ同じ型番の同じ製品であっても、どこかが微妙に違っているから、たがいに区別が可能である。一方、個々の電子は、たがいに区別が不可能である。いくら区別しようとしても、本質的に区別が不可能なのだ。ただし、観測した時点で、電子はその位置にあることが確定したから、その時点で電子は区別されたことになる。
つまり、観測とは、「たがいに区別不可能なもの」から、「たがいに区別可能なもの」へと、転じることなのだ。それが数学的な意味合いだ。
電子が電子銃から発射された時点では、電子は区別可能なものとして確定されている。しかし、電子銃から発射されたあとでは、もはや区別不可能なものとなる。空中を移動しているらしい電子は、最初の電子なのか、あるいは、玉突き状態で動いた電子なのか、区別できない。二重スリットを通過している間も、電子はたがいに区別できない。
ただし、途中、二重スリットのどちらか片方を通過する時点で、電子が観測されることがある。この場合、観測された時点で、電子は区別可能なものとなる。つまり、考察対象が、「波」としてのものから、「粒子」としてのものへ、切り替えられる。その後は、粒子はふたたび波動関数で計算されるだけなので、粒子はふたたび「区別不可能なもの」と見なされる。そして、最後に、感光板に達すると、あらためて「区別可能なもの」に切り替えられる。
なお、途中観測の有無についても、考察できる。電子銃が感光板に達するまでの途中で、二重スリットのところで、どちらのスリットを通るか、観測することができる。すると、途中で観測した場合と、途中で観測しない場合とでは、最終的な結果が異なるのだ。では、それは、なぜか?
コペンハーゲン解釈では、「観測が現実に影響する」というふうになる。つまり、「観測することで、波動関数が収束する」というわけだ。
二重空間モデルでは、そうではない。かわりに、次のように説明する。
「途中で観測した場合と、途中で観測しない場合とでは、まったく別の事象なのである。まったく別の事象であるから、まったく別の実験結果が出るのは、当然である」
では、なぜ、まったく別の事象であるか? それは、途中で、考察対象を変更したからだ。
途中観測なしの場合には、粒子は出発点にあるだけだった。一方、途中観測ありの場合には、二重スリットのところで、粒子は新たに出現した。──かくて、両者はまったく別々の事象となった。
要するに、途中観測の有無は、存在確率を変えたのではなくて、事象そのものを変えたのだ。
こういうことは、不自然に思えるかもしれない。しかし、こういうことは、確率では、別に不思議ではない。たとえば、次の例がある。
「コインを2枚投げて、そのうち1枚以上が裏」
という確率は、確率論によって計算される。一方、
「コインを2枚投げるとして、途中の1枚目までを実行した時点で、盗み見する。裏か表かが判明する。判明したあとで、それぞれの場合ごとに、最終的な結果を計算し直す」
というやり方だと、事象はまったく異なってしまう。ここでは、観測という出来事によって、事象がまったく別の事象になってしまったのだ。
それでも、物理学者は、こう主張するかもしれない。
「コインをトスするという物理現象は、どちらにしても、同じである。同一の物理現象に対して、異なる計算結果が出るとしたら、観測という行為が確率に影響したのだ」
と。馬鹿げた話だ。この伝で言うと、「観測がコインの裏表を決定する」とか、「観測がサイコロの出る目を決定する」とか、そういう理屈になる。
本当は、そうではない。途中で観測したことで、事象がまったく別の事象になってしまったのだ。それだけのことだ。
もっと簡単に示そう。一枚のコインをトスして、伏せる。裏表の確率は、五分五分だ。ところが女児が、こっそり盗み見る。裏表が、彼女には判明する。すると、物理学者は、こう主張する。
「彼女の観測によって、裏表は決定された。コインの裏表を決めるのは、観測である」
一方、別の物理学者はこう主張する。
「私は彼女の観測結果を聞いていないし、私自身も観測していない。ゆえに、裏表は決定されていない」
これを聞いて、論理学者は、こう主張する。
「観測者がいるかいないかで命題が異なるのだとしたら、地上のあらゆる人間について、観測したか否かを調査しなくてはならない。コインの裏表を決めるのが、人間が観測したか否かであるとしたら、地上のあらゆる人間を観測しなくてはならない」
こうなると、ほとんど論理矛盾である。さらには、観測した人間が(事実とは逆の)嘘を報告したり、誤認したりすることもある。こうなると、もうメチャクチャだ。……最も単純な場合でも、「観測してないものを観測したと誤認する」ということは十分にあり得るし、その場合は、観測が事実とは逆のことを決定することになる。おかしい。
では、正しくは? 「決定」と「判明」とは別のことだ、ということだ。事実の世界で何かが決定することと、人の意識のなかで何かが判明することとは、別のことなのだ。それらは別の世界(数学世界)のことであり、純然と区別される。なのに物理学者は、この両者を混同する。そしてたちまち、思考が混乱したすえ、頭の回路まで混乱してしまうのだ。
( ※ より詳しい説明は、後述する。 → 該当箇所 )
氏 名 南堂久史
メール nando@js2.so-net.ne.jp
URL http://hp.vector.co.jp/authors/VA011700/physics/2slits.htm (本ページ)
[ THE END ]