|
| ___ |
注釈編 波のようにふるまう 水面波 経路とは何か 複素数の波 波動関数と存在確率 シュレーディンガー方程式 くりこみ理論 |
目次 | | | | | | | | | | | | | |
発展編 物理空間と数学空間 異なる数学空間 確率とは何か 確率と干渉縞 波から粒子への転換 素粒子の質量とは何か 結語 観測と誤認 二重空間モデル 二重空間モデルの図式 観測とは何か |
「量子の世界では、一つの粒子が波のようにふるまう」という解釈もある。これは、よくある解釈だが、正しくない。
この解釈では、粒子はあくまで粒子である。二重スリット実験については、実験結果として干渉縞が現れることだけを主張する。そして、二重スリットの通過については、やはり、「一つの粒子が、どちらか一方のスリットだけを通る」と主張する。
とはいえ、そういう発想だと、「粒子を一つずつ発射する」という場合には、干渉が発生しないことになる。矛盾。
だから、「一つの粒子が波のようにふるまう」という解釈は成立しないのだ。このことが、二重スリット実験の核心である。外村の実験は、「粒子が波のようにふるまう」という解釈を、実験レベルではっきりと否定したわけだ。(理論レベルでは、最初のころから判明していたことだが。)
さて。「一つの粒子が波のようにふるまう」という解釈は否定された。そこで、多くの物理学者は、別の解釈を出した。それは、「一つの粒子が二つのスリットを通る」という解釈だ。しかし、それだと、言語的に矛盾が起こる。しかも、以下の「補足」に見るような論理矛盾も起こる。だから、「一つの粒子が二つのスリットを通る」という解釈も、成立しないのだ。
( ※ 一方、本論は、「二つのスリットを通る」という述語部分は肯定するが、主語部分について、「一つの粒子が」というのを否定して、「波としての量子が」というふうに認識する。)
ちょっと注釈しておく。(読まなくてもいい。)
「近似」と聞くと、「近似の手法なんかどうだっていい」と思う読者もいるだろう。特に、数学系の人は、近似処理なんかを馬鹿にするだろう。しかし、実は、物理の問題というのは、ほとんどが近似処理の問題なのだ。基本的な原理は判明しているから、その基本的な原理の上に、いかに有益な体系を築くか、ということが問題となる。
たいていの場合、条件があまりにも複雑なので、近似しないと、何も答えが出ない。そこで、近似する。すると、近似の仕方に、各人の差が現れて、各人の業績となる。「××氏は××法という近似処理を提唱したので、その名を残す」というふうに。それでノーベル賞ももらえる。たとえば、ファインマンの経路積分も、朝永のくりこみ理論も、その手の業績だ。
とにかく、物理学というのは、そういうものなのだ。抽象的な演繹処理より、現実との合致を重視する。
水面波の波紋については、本文中では詳しく記述しなかったが、簡単に説明しておこう。
二重スリットを通るのが水面波であったとしよう。すると、水面波は、発射点から二重スリットへ、弧を描いて伝わるように見える。ただし、ここでは、弧の形で力が伝わるわけではない。力そのものは、水面の全体に伝わる。ただし、伝わるには時間が必要だ。そこで、一定の時間ごとに等高線を引くと、弧の形になる。
では、いったん力が伝わったあとは、どうなるか? その後は、力の影響で、振動が発生する。そして、水面の各点の振動による力が相互に影響しあう。それらのさまざまな力の合成として、現実の波紋は決定される。
とすれば、二重スリットに届いた力は、発射点から直接届いた力だけではなくて、水面の各点からの力の総和として決定される。
このことを拡張する形で、「われわれの宇宙の各点は、それぞれ、宇宙全体の影響を受けている」と主張する人もいる。しかし、これは、正確ではない。
第1に、各点に届く力は、一定の範囲内の力に限られる。その範囲は、波の伝達の速度によって制約される。発射点Aと二重スリットBとの間の途中点をPと書くと、距離APと距離PBとの和が、一定の長さに収まっている必要がある。換言すれば、はるか遠くの宇宙の存在が、われわれの住んでいる世界に影響することはない。(絶対に影響しないのではなくて、影響するためにはものすごい時間がかかるので、時間切れとなる。)
第2に、距離が離れれば離れるほど、力の影響は弱まる。点Pが遠ければ遠いほど、その影響は弱まる。通常、ホワイトノイズに掻き消されてしまう。ゆえに、事実上、無視して構わない。
以上の二つの点で、制約が加わる。ただし、この制約から逃れるのであれば、水面波の比喩はかなり適切だ。つまり、一定範囲内の領域であれば、水面波の伝播と波動関数の伝播は、ほぼ同じものだと発想してよい。それが本論の立場であり、その具体的な方法がファインマンの経路積分だ。
( ※ ただしファインマン自身は、経路積分を、波のようなものだとは述べていない。あくまで粒子のふるまいとみなしており、経路に揺らぎが生じると考えているだけだ。コペンハーゲン解釈に従いながら、粒子の存在確率を雲のように見なすかわりに、粒子の経路の揺らぎを考えているだけだ。一方、本論は、考察対象は「粒子」でなくて「波」であると見なす。とはいえ、その数学的な扱い方が、ファインマンの経路積分にそっくりになるわけだ。……興味のある人は、水面波の動きを計算してみるといいだろう。ついでに、水の粘性などを考慮して、コンピュータでシミュレーションしてもいいかもしれない。)
( ※ なお、水面波との比較で言うと、「波動の伝わる速度は有限である」という結論が大事である。すぐ上で「伝わるには時間が必要だ」と述べたことが、これに相当する。)
波の伝わる経路とは、何のことか? コペンハーゲン解釈では、経路は、「粒子の存在確率」を示すものとして理解される。本論の解釈では、経路は、「波の伝わり方」を示すものとして理解される。
たとえば、筒の内側のような形状(雨どいのような形状)があったとする。左右方向には凹型であり、上下方向には直線的である。ここで、直線方向で、点Aから点Bに、球を転がすとする。
A ────→ B
球は、点Aから点Bへと、最短距離をたどって、まっすぐ進むかもしれない。あるいは、途中でちょっと脇にぶれてから、また中央に戻って、Bに達するかもしれない。さまざまな場合が考えられるが、実際には、どうか?
この原稿の古いバージョンでは、「球の通りやすさ」というものを想定した。しかしこれは、コペンハーゲン解釈の「存在確率」というものに毒された、誤った判断であった。正しくは、以下の通りだ。
ファインマンの経路積分では、「出発点と到着点の間のあらゆる経路を取る」と想定される。これが正しい。
ただし、もっと正確に言えば、「水面の波の伝わり方」と同様である。つまり、ホイヘンスの原理の通りだ。具体的に言えば、次の通り。
一つの波面上で、すべての点が波動の中心となって、それぞれ二次波を出す。これら二次波の合成として、現実の波が定まる。つまり、二次波の包絡面が、次の波面となる。こうして次々と波が進んでいく。
各点ごとに考察すれば、各点に到達する振動全体の合成として、各点の挙動が決まる。
「経路とは何か?」という問いに対しては、以上のことから、容易に答を得られるだろう。それは一定の線ではなくて、平面上の広がりをもつものなのだ。その広がりは、刻々と変動していくので、簡単に「これ」というふうには示せないが、計算で示すことはできる。その示し方が、ファインマンの経路積分だ。
( ※ 現実に計算するには、近似法などで、いろいろとテクニックを要する。ただし、ファインマンの経路積分の発想さえあれば、コンピュータで近似すれば、かなり精度のいい近似を得られるだろう。なお、ここでは、波が複素数であるというところが、水面波の場合とは違う。注意。)
以上では、「波」という用語を用いたが、ここでいう「波」は、電磁波のような実在する波ではない。実在する波は直接的に計測することができるが、量子の「波」は直接的に計測ができない。この波は、複素数で示される波であり、また、演算子を用いて記述される。
その意味で、水面波のような「はっきりと目に見える波」ではなくて、理論上の波にすぎない。その点は、混同しないようにしよう。
なお、水面波との違いを言えば、水面波は実数で示され、量子力学の波は複素数で示される。前者は現実世界において三角関数(サイン・コサイン)で観測され、後者は現実世界において存在確率のように観測される。
( ※ もっと詳しい話を知りたければ、量子力学の教科書を参照のこと。)
( ※ 電磁波は、複素数波でなく、実数波である。どちらも空間を伝わるという点では似ているが、複素数と実数という違いがあるわけだ。ただし、どちらも、真空中を伝わる、という点では似ている。その点では、水面波とは異なる。)
( ※ 本項のような発想は、実は、本質を突いている。「マックスウェルの方程式がどういうふうにして誕生したか」という歴史的な話を、電磁気学の本などで調べるといいだろう。マックスウェルが方程式の前に想定したのは、「エーテルの微細な渦動」というモデルである。このモデルが、「量子からなる真空における複素数波の実数部分」に相当するのだ、と考えるとよさそうだ。……たいていの人は、マックスウェルの方程式を「天下り的に与えられたもの」と思いがちだし、方程式の意味なんかを考えたりしないものだが、実は、マックスウェルの方程式の根底には、「真空とは何か」という核心が横たわっているのだ。)
( ※ 余談だが、「目に見える」という表現は、比喩である。「可視光線で見える」という意味ではなくて、「電波やX線などが計測器で検出される」という意味。言わずもがなだが。)
「波動関数で存在確率を示せる」という主張は、それ自体は、間違っているとも言えない。というのは、感光板における存在確率は、まさしく波動関数で示せるからだ。ここでは「存在確率」という言葉を使ってよい。というのは、主語は「粒子」としての電子であるからだ。
ただし、途中の空間においては、「存在確率」という言葉を使うべきではない。というのは、主語は「粒子」としての電子ではないからだ。途中の空間においては、「波」だけがあって、「粒子」はないのだから、(粒子の)「存在確率」という言葉が無意味になるのだ。
波動関数で「存在確率」が明らかになるというのは、間違ってはいないが、話は感光板だけ(観測されるものだけ)に限られる、という点に留意しよう。
特に、コペンハーゲン解釈における「波動関数が収束する」という表現は、まったくの間違いだ。この表現では、「発射点と到達点の間で、波動関数(または存在確率)が雲のように分布している」ということになる。そんなことはない。発射点と到達点の間では、波動関数は複素数の波であるから、波動関数は目に見えない。もちろん、「存在確率の雲」なんてものも存在しない。当然、存在しないものが、あとで収束する、ということもない。正しくは、こうだ。
・ 発射点と到達点の間では、波動関数は、複素数の波である。
・ 到達点(観測平面)でのみ、存在確率が波動関数で計算される。
要するに、波動関数はあくまで複素数波(目に見えないもの)であって、それがただちに存在確率(目に見えるもの)になるわけではないし、また、存在確率が雲(目に見えるもの)のようになって空間を伝わるわけでもない。
数学的に言えば、複素数波が「波動関数の絶対値の二乗の区間積分」という形を取るときに、複素数波から存在確率へと転換する。そのとき、目に見えるようになる。
なお、そういう転換を途中経路でする場合には、途中経路における存在確率を計算できる。とはいえ、観測しない限りは、波動関数は複素数波のままであって、存在確率に転換しない。もちろん。
( ※ 波動関数から存在確率への転換については、後述する。 → 「 粒子から波への転換 」
シュレーディンガー方程式は、何を意味しているのだろうか?
通常は、「ただの仮定だ。いちいち考える必要はない」というふうに、質問はあっさり却下される。ま、それでも演繹的な体系を構築することはできるから、それはそれでいいのかもしれない。しかし、その仮定がどういう意味をもつかを理解しないと、どうにも気持ち悪い。たとえば、ユークリッド空間の体系を理解するとき、公理系を示す「平行」などの用語を、単に無定義語としても、数学的な体系を構築することはできる。とはいえ、「平行」などの用語の意味をはっきりと理解しておけば、もっと深い理解ができるはずだ。物事の本質を探りたければ、そういうことを知りたくなって当然だ。なぜなら、物理学者が知りたいのは、記号の羅列としての演繹的な数学空間ではなくて、この宇宙の物質的な真実であるからだ。
では、シュレーディンガー方程式は、本質的には、何を意味するのか? コペンハーゲン解釈で言えば、「粒子の存在確率を示すもの」であろう。しかしすでに示したように、そういう発想は否定される。本論の発想に従えば、次のようになる。
シュレーディンガー方程式とは、空間の振動状態を与える式である。それは、水面波の方程式に似ている。もともとある空間(いわば水面)は、どのような振動状態にもなることが可能だ。ただし、最初に発生する衝撃が問題だ。最初の衝撃が、電子の発射であることもあり、光子の発射であることもある。それぞれに応じて、波動が伝わり、空間全体が振動する。ここでは、波動の伝わり方が問題だ。それを知りたい。そして、その答を与えるのが、シュレーディンガー方程式だ。というのは、最初の波動に対して、空間全体に生じる振動は、一意的に決まるからだ。そして、それを決めるための条件が、シュレーディンガー方程式だ。
たとえば、電子として ◯ が発射される。このとき、これに共振するのは、たくさんある ◯ だけである。一方、小さな ◯ や、大きな ◯ は、周期が異なるので、共振することはない。ここで、どの ◯ が共振するかということを条件づけるのが、シュレーディンガー方程式だ。電子の場合には、たくさんある電子だけが共振して、空間全体の電子・反電子が振動しながら、波が伝わる。光子の場合には、たくさんある光子だけが共振して、空間全体の光子が振動しながら、波が伝わる。(これは比喩的な表現だ。実際に電子・反電子などの粒子が発生する必要はない。実際には波だけがある。)
繰り返して言う。シュレーディンガー方程式とは、粒子の存在確率を与えるものではない。空間の振動状態を与えるものだ。そして、その振動が空間を伝わったあとで、最終的に観測装置に伝わると、そこにおいて、粒子の存在確率の形で、観測される。ここでは、粒子の存在確率が空間を伝わっているのではない。波が伝わってから、観測装置において、波が粒子の存在確率に転化したのだ。シュレーディンガー方程式が教えるものは、あくまで波であって、観測された粒子ではないのだ。このことを混同しないように注意しよう。
量子論には、「無限大の発散」という問題がある。たとえば、電子を大きさゼロの質点と仮定すると、エネルギーが無限大になってしまう。しかるに、現実の電子は、エネルギーは有限の値である。つまり、量子論と現実とが矛盾する。そこで、この矛盾を解決するために、無限大のかわりに、現実に観測された値を当てはめる。そうすると、あとは矛盾なく解決することができる。──これが、くりこみ理論の要点である。そのことを具体的に数式で説明したのが、くりこみ理論そのものだ。(朝永・シュウィンガー・ファインマンの業績。)
とはいえ、「理論ではうまく行かないから、現実の値を当てはめる」というのは、あまりにも御都合主義に思える。本当は、いったい、どういうわけなのか?
実は、この問題は、本論の立場に立てば、すっきりと説明が付く。それには、前述の ◯ がたくさんあるモデルを使えばよい。
このモデルでは、波として作用するのは、 ◯ と ◯ がぶつかっている範囲だけだ。そのようなぶつかりあいの作用には、最小限界がある。つまり、量子の半径を r と書いたとき、r+r つまり 2r (量子の直径に相当する)が、最小限界となる。
この値よりも距離が短くなると、ぶつかり合いは生じなくなる。つまり、距離が短すぎて、ぶつかろうにも、ぶつかれなくなる。正確に言えば、量子と量子の相互作用はなくなる。
だから、最小限界よりも短い距離では、 ◯ と ◯ がぶつかりあう形の「波」は生じない。つまり、 ◯ と ◯ との関係は、「波」として扱えない。となると、「波」であることを前提としたシュレーディンガー方程式は、成立しなくなる。
一方、最小限界よりも短い距離では、量子の位置はほとんど確定しているから、粒子として扱っていい。粒子として扱うならば、観測された値を使えばよい。(なぜなら、粒子とは「観測されたもの」のことであるからだ。)
かくて、くりこみ理論の本質は、以上のような短い平易な文章で説明されたことになる。
なお、少し前の「シュレーディンガー方程式」のところで説明したことを思い出そう。シュレーディンガー方程式とは、空間の振動状態を与えるものだ。このことと、本項のことを、合わせて考えると、次のように言える。
「空間は、連続的ではない。最小限界よりもずっと大きな範囲を考えると、最小限界は無視できるので、空間を連続的と見なすことができる。しかし、最小限界よりも小さな範囲を考えると、空間は連続的ではなく離散的である」
つまり、電子や光子などだけが「量子化されている」(離散的である)わけではない。空間そのものが「量子化されている」(離散的である)のだ。── このことが、くりこみ理論の話題から、推察される。
数学世界における実数空間は連続的だが、物質のある宇宙空間は量子化されているのである。
( ※ なお、「空間の量子」というものを考えるのは、無意味である。なぜなら、最小限界を定める r という値は、一定の値が固定的に決まっているわけではなくて、電子や光子などで、異なるからだ。量子が変われば、それぞれの r が別々に定まる。たとえば、電子の r と中間子の r は、同じではない。……ここでは、空間が量子化されているということを、概念的に理解するだけでいい。)
二重空間モデルでは、一つの物理空間に対して、二つの数学空間が対応する。そして、それぞれの数学空間が切り替えられる。つまり、物理空間と数学空間との対応関係が変更される。
これは、不自然に思えるかもしれない。先の例では、「確率の場合も同様だ」というふうに説明したが、この説明では、根源的な説明となっていない。そこで、根源的に説明しよう。
物理空間というのは、現実世界のものだ。数学空間とは、現実世界を簡略してモデル化した空間だ。この両者は、「現実と理論」という対応関係になっている。とすれば、一つの現実に対して、複数の理論が対応することになる。
このことは、一見、不自然に見えるかもしれない。しかし、このことは、実は、物理学の基本原理なのである。ここで、「数学空間」というのを、「法則」と言い換えてみれば、すぐにわかる。
現実の物理空間というのは、常に一つである。(多世界解釈を除けば。)一方、現実の物理空間を描写するためには、さまざまな物理法則が知られている。たとえば、次のように。
・ 万有引力の法則 (ニュートン方程式)
・ 電磁気学の法則 (マックスウェル方程式)
・ 量子力学の法則 (シュレーディンガー方程式)
などだ。これらの物理法則は、一定の方程式で表現される。そして、一定の方程式を満たすものは、一定の数学空間となる。だから、結局、(一定の方程式を満たすような)数学空間が、現実の物理空間を描写するための数学空間となっている。
これらの数学空間は、考察の場合ごとに、対応するものが選ばれる。たとえば、万有引力を考えるときは、ニュートン方程式を取るが、それはつまり、現実の物理空間を「ニュートン方程式を満たす数学空間」として認識していることになる。
もっと典型的な例もある。現実の物理空間は、それぞれ、次の数学空間で認識できる。
・ 古典力学による、三次元のユークリッド空間
・ 特殊相対論による、三次元と一次元の「時空」の空間
・ 一般相対論による、重力場の空間(非ユークリッド空間)
現実の物理空間はただ一つだが、それに対応する数学空間はいろいろと考えられる。これらのうち、どれかが正しいとか間違っているとかいうわけではなくて、「簡単なものは単純化された近似になっている」というだけのことだ。
話を戻そう。確率の場合で言えば、上記の場合とは順序が逆になる。つまり、現実の物理空間を簡略化したモデルとして、確率の数学モデルがあるのではない。確率の数学モデルが先にあって、その数学モデルに従って予想してから、現実の物理空間がどうなっているかを確認する。たとえば、「コインをトスすると裏表が半々だ」というふうに数学モデルを提出してから、現実にコインを何十回かトスしてみて、現実が理論通りになっているかを検証する。
量子力学の場合も、同様だ。(量子理学の世界は確率的な世界なのだから、当然だが。)たとえば、「アルファ粒子が一定時間のうちに崩壊するのが検知される確率は、これこれの値だ」と確率的に予測してから、現実の物理空間で観測する。ここでは、確率で結論したのは、理論的な数学空間における値であり、観測したときに判明するのは、現実の物理空間における値である。この両者は、まったく別の世界の値だ。ただし、一定の対応関係が付く。
一般に、量子力学の世界で計算によって結論される値は、すべて、理論的な数学空間における値である。観測したときに判明する値は、すべて、現実の物理空間における値である。両者はまったく別の世界のことだ。そして、この両者を結びつけるのが、物理学者だ。とはいえ、その結びつけは、あくまで、物理学者の判断である。結びつけてもいいし、結びつけなくてもいい。また、結びつけ方も、いろいろあっていい。たとえば、ある物理学者は、シュレーディンガー方程式を使って、昔の電子の定数を使って、小数第二位まで手動で計算した値を出した。別の物理学者は、ハイゼンベルクの行列式を使って、最新の電子の定数を使って、小数第百位までコンピュータで計算した値を出した。両者の値は、微妙に異なる。では、どちらが正しいか? ──そんなことを考えても、無意味だ。理論と現実との結びつけをするのは、それぞれの物理学者の個人的な判断である。既存データや計算方法などの時代背景に応じて、いろいろと異なる理論結果が出るが、どちらが正しいかなんてことを考えても、ほとんど意味がない。意味があるのは、観測結果と照合して、「どちらが正確か」ということだけだ。通常、昔の理論よりは、今の理論の方が正確だ。今の理論よりは、未来の理論の方が正確だ。そんな正確さを競っても、意味がない。大切なのは、「現実と理論との対応関係は、いろいろと成立する」ということだ。
二重スリットの場合も同様だ。電子線を発射したあと、干渉縞が生じる。その干渉縞がどういうものになるかは、近似の仕方によって、計三者(過去・現在・未来)ごとに、微妙に異なる計算結果を出すだろう。ただし、そのすべては、理論の世界のことだ。一方、理論なんかを知らなくても、どこかの子供が感光板を見れば、感光板の状態を知ることができる。ここでは、理論的な値が急激に収束したのではなくて、理論とは無関係に、現実世界のことが判明したわけだ。そのあと、この現実世界に対応する理論を求めて、それぞれの計算結果をいろいろと調べてもいいが、別に、調べなくてもいい。とにかく、理論としての数学空間と、現実としての物理空間は、まったく別のものなのだ。その違いをはっきりと理解しておこう。
( ※ ここを混同すると、「理論の世界だけで波動関数が収束した」というふうに誤解する。それがコペンハーゲン解釈だ。)
現実の物理空間には、複数の数学空間が対応する。(すぐ前に述べたとおり。)
ここで、複数の数学空間というのは、通常は「方程式の違い」で表示されるだけだが、もっと根源的に、「数の種類の違い」で表示することもできる。たとえば、次の区別が可能だ。
・ 実数の空間
・ 自然数の空間
このように区別すると、量子力学はきわめてシンプルに表現できる。なぜか? 自然数は、実数のなかの特定の値ではなくて、別の数学空間に属することになるからだ。
通常の発想では、自然数とは、実数のなかにある、とびとびの値である。しかし、現実の世界を見ればわかるとおり、そんなことでは当てはまらない現象がある。たとえば、猫を数えるときには、「1匹、2匹、3匹、……」というふうに数えるのであって、「1.5匹」とか、「3.14匹」とか、中途半端に数えることはない。ここでは、中途半端な数は、もともと存在しないのだ。同様に、電子や中性子なども、「1個、2個、3個、……」というふうに数えるのであって、「1.5個」とか、「3.14個」とか、中途半端に数えることはない。ここでは、「1、2、3……」という値は、とびとびの値なのではなくて、もともとそういう値しかないのだ。「1.5」という値を飛び越えているわけではなくて、もともとそんな中間的な値はないのだ。
現実の三次元物理空間の距離は、実数によって描写される。そこでは、尺度となる数は実数である。一方、猫の匹数や量子の個数は、自然数によって描写される。そこでは、尺度となる数は自然数である。つまり、前者の空間は実数空間(R 3)であり、後者の空間は自然数空間(N 1)だ。──こういうふうに別々の数学空間として認識すると、「とびとびの値を取る」という概念そのものが不要となる。要するに、量子化されるような数は、「とびとびの値を取る」というふうに何らかの条件が付けられているのではなくて、単に「現実の物理空間に対応する数学空間が自然数の空間である」というだけのことにすぎないのだ。
元はと言えば、「数学的な数は、原則として実数だ」という発想そのものが、古典的な発想なのである。数学的な数は、自然数のこともあるし、実数のこともあるし、複素数のこともあるし、循環的な群の数であることもある。それぞれは別の数学空間をなす。そして、現実の物理空間が、どの数学空間に対応するかは、場合ごとに異なるのだ。たとえば、次のようになる。
・ 量子論的な個数 (自然数)
・ 三次元ユークリッド空間 (実数)
・ 相対論的な時空の空間 (複素数)
・ 量子論の波動関数 (複素数)
・ 化学的な元素の周期律 (8を法とする群)
もっと面倒くさいことをやりたければ、数学にはさまざまな数学空間(多様体やら何やら)があるから、その数学空間に該当する現実の現象を見出すこともできるだろう。たとえば、特異点なんてものを考察して、ブラックホールに当てはめる例もある。
こういうふうに、現実の物理空間に、さまざまな数学空間を対応させることができる。そしてまた、そう考えると、「とびとびの値」なんてものを考えることは不要になる。
「確率とは何か」という問題を考えよう。
数学的には、確率は、「確率空間の公理を満たすもの」というふうに定義される。しかし、これは、数学的に確率と呼べるものの定義を与えているだけであって、その元となる現象を本質的に示しているわけではない。ただの形式論にすぎない。ほとんど役には立たない。(「確率とは何か」がわかったあとでなら役立つが、わかっていない段階では役立たない。)
ここで、コインのトスを考えよう。コインをトスすると、裏表が半々となる。これを古典力学的に分析すれば、裏か表かは、各回ごとに厳密に決定されるはずだし、予測可能であるはずだ。ところが、現実には、そうならない。なぜか? ごく微小な力の揺らぎがあって、その揺らぎが最終的な結果を大きく左右するからだ。
この揺らぎは、通常、ホワイトノイズとして理解されるが、実は、ホワイトノイズである必要はなく、周期のある波であってもよい。たとえば、コインのトスに対して、周期のある波が裏表を決定するとすると、やはり、裏表は半々になるだろう。ただし、周期のある波が裏表を決定するとなると、裏表もまた、周期的になる。裏を ■ で示し、表を □ で示せば、次のようになるだろう。
■□■□■□■□■□■□ …… (1周期)
または
■■□□■■□□■■□□ …… (2周期)
のように。この場合も、裏表は確率的に半々となる。ただし、周期性もある。
もちろん、現実には、このような周期性は見られない。そのことから、コインの裏表を決定する力の揺らぎは、ホワイトノイズである、と推察される。
一方、二重スリットの場合は、どうか? 確率は、干渉縞となって現れる。ここでは、二重スリットでなく単スリットの場合を見て、「(空間的に)周期性がある」と判断される。正確に言えば、こうだ。
「電子の波長と、スリットの幅とが、ほぼ同じである。そのせいで、分布に一定の山と谷が現れる」(回折現象)
つまり、「電子を通すときの空間の振動数」によって決まる「電子の波長」が、「スリットの幅」とほぼ同じになったときに、空間の振動によって生じる周期的な揺らぎが、確率波となって干渉縞を作るのである。
ただし、この周期性は、長期的に統計を取った場合にのみ、判明する。現実の個々の場合には、はっきりとした周期性がない。ということは、力自体は周期的だが、そこにホワイトノイズのような揺らぎが加わっていることになる。
つまり、空間の振動自体は、きれいなサインカーブのようなグラフで描けるのだが、そこに揺らぎとしてのホワイトノイズが加わって、ごちゃごちゃしたサインカーブのようになっている。そのホワイトノイズのせいで、現実の個々の場合(ホワイトノイズとサインカーブとの合成)がどうなるかは、一意的に決まらない。とはいえ、長期的に統計を見れば、ホワイトノイズの影響は無視できて、サインカーブの部分だけが残る。
以上が、確率の本質だ。つまり、「長期的には、はっきりとしたことが関数で表示できるが、個々の場合には、一意的に決まらない」ということは、「関数とホワイトノイズの合成」という形で理解できる。
こう理解すると、古典力学と量子力学の違いも、はっきりする。古典力学とは、ホワイトノイズを無視した関数である。巨大なマクロ的な世界の場合には、関数の力が大きいので、ホワイトノイズを無視できる。一方、微細なミクロ的な世界の場合には、関数の力が小さいので、ホワイトノイズを無視できない。かくて、古典力学の世界は決定的となり、量子力学の世界は確率的となる。
( ※ ホワイトノイズの存在を、「不確定性原理」と理解すると、直感的にわかりやすくなる。)
「確率とは何か」を理解すると、二重スリット実験において、干渉縞が発生する理由もわかる。
前項で述べたように、個々の場合に感光板で観測される粒子がどうであるかは、そのときの関数とホワイトノイズとの合成によって決まる。この実験の場合には、関数は、サインカーブと見なしてよい。その関数とホワイトノイズとの合成によって、現実に観測される電子の位置が決まる。
さて。長期的には、ホワイトノイズを無視していい。というわけで、ホワイトノイズを無視して、サインカーブの関数だけで考えよう。すると、空間の振動状態が、サインカーブの、山であったり谷であったりするごとに、現実に観測される粒子の位置は、山に対応する位置であったり、谷に対応する位置であったりする。つまり、位相がある。(なぜそうなるかといえば、前述の通り。つまり、電子の波長と、スリットの幅とが、ほぼ同じであるせいで、振動の影響が大きく現れる。)
つまり、干渉縞が現れるのは、スリットの部分で、空間の振動があるからなのだ。その空間の振動が拡大されて、効果が重なりあうと、(位相差のせいで)、干渉縞となるわけだ。
ここで、注釈しておこう。この振動は、実数の振動ではなく、複素数の振動だ。また、存在確率を左右するような振動だ。仮に、音波や水面波のような実数エネルギーの振動であれば、干渉縞は、実数エネルギーの干渉縞となる。具体的には、振幅の干渉縞となる。
さて。音波や水面波では、実数エネルギーの干渉縞が現れる理由は、何か? もちろん、二つの振動で、山と山が強め合ったり、山と谷が打ち消しあったりするからだ。── このことから、複素数の場合にも、類推ができる。存在確率の山と谷ができる(干渉縞ができる)のは、発生と発生が強めあったり、発生と消滅が打ち消しあったりするからだ。たとえば、発生と発生が強めあうと存在確率が高くなり、発生と消滅が打ち消しあえば存在確率が低くなる。かくて、干渉縞が発生する。
逆に言えば、存在確率を意味する干渉縞が発生することから、真空という空間において「発生と消滅」という形の振動が起こっているはずだ、と推定されるわけだ。……これはかなり重要な結論である。
「確率とは何か」を理解すると、「波から粒子への転換」とはどういうことか、ということもわかる。
「波から粒子への転換」とは、「波動関数から存在確率への転換」のことだ。では、それは、何を意味するか?
波動関数は、存在確率を伝えるのではない。波動関数は、あくまで複素数波であって、目に見えるものではない。ただし最終的には、波動関数が、何らかの形で(つまり粒子の形で)観測される必要がある。
ここで、問題が生じる。観測される粒子は、数学的に、自然数空間に属する。つまり、「1個、2個、3個、……」というふうに数えられる。個数が多いときには、多数のものがなめらかに分配されるので、連続した実数と見なしてもいいだろう。(だから干渉縞などが現れる。)
ところが、実際に一個一個の粒子を発生させる力は、波動関数であり、これは、1個の粒子を生み出すためには、力が弱すぎる。たとえば、1個の電子を生み出すためには、1個の電子に相当するエネルギーが必要だが、しかるに、(1個だけの電子を発射したときの)波動関数が感光板のどこかに及ぼす力は、それよりは弱い。つまり、「少なくとも1個以上の電子を発生させる」というこふうにはならない。ただし、ホワイトノイズがあるせいで、波動関数とホワイトノイズとの合成が、1個の電子を生み出すエネルギーに達する。そのとき、形に表れなかった電子が、形を取って現れる。つまり、波としての波動関数が、粒子に転換する。
この転換が起こるかどうかは、ホワイトノイズに依拠する。波動関数のエネルギーが十分に大きいときには、ホワイトノイズを無視してよい。しかし、波動関数のエネルギーが小さいとき(一個の電子を生み出すのに足りないとき)には、ホワイトノイズの揺らぎによって、電子が発生したり発生しなかったりする。── この最終結果の頻度が、「存在確率」だ。
《 波の規模が大きいとき 》
【 空間 】 【 感光板 】
複素数波の伝播 ──→ たくさんの粒子が分布する
《 波の規模が小さいとき 》
【 空間 】 【 感光板 】
複素数波の伝播 ──→ 一つの粒子が確率的に発生する
要するに、波動関数は、存在確率の波ではない。ただの複素数波である。それが感光板で、存在確率に転換する。そして、その転換が起こる理由は、こうだ。
「波の規模が小さいときには、複素数波のもたらす力は小さな連続数である。一方、粒子の個数は 1 または 0 でしかありえない」
仮に、粒子の個数が 1 または 0 のかわりに、( 0.67 のような)小数の数を取れるのであれば、小数の粒子(砕けた破片のような粒子)が、数式に従って分布するだろう。しかし現実には、粒子の個数は 1 または 0 でしかありえない。砕けた破片が分布することはありえない。そこで、そのたびごとに、あちらに発生じたり、こちらに発生したりする。どこに発生するかは、ホワイトノイズしだいなので、あらかじめ予測はできない。ただし、何度も何度も繰り返せば、ホワイトノイズの影響を無視できるので、数式に従って多数の粒子が分布する。
結局、ここでは、「二つの数学空間がある」というのが、本質的な原理となっている。「波」から「粒子」に転じるときに、数学空間が「波」の数学空間から「粒子」の数学空間に転じるが、そのとき、数学空間の種類の違いのせいで、粒子は、破片の形では分布せずに、存在確率の形で分布するわけだ。── そのことが特にはっきりするのが、波の規模が小さい場合である。(逆に、波の規模が大きい場合には、確率で理解するかわりに、多数の粒子の連続的な分布として理解してもいい。)
前項では、「1個の電子を生み出すためには、1個の電子に相当するエネルギーが必要だ」と述べた。ここで必要とされる量のエネルギーが、粒子の質量に相当する。そう考えていいだろう。
波から粒子に転じるとき、いつでも自由に転じることができるわけではない。1個の粒子が発生するためには、1個の粒子に相当するためのエネルギーが必要だ。それが最小単位となる。そして、その最小単位は、素粒子(量子)の種類ごとに決まっている。電子ならばこれこれ、陽子ならばこれこれ、パイ中間子ならばこれこれ、というふうに。
つまり、「波 → 粒子」という転換のときには、区切りの枠となるような(エネルギーの)最小単位があるわけだが、その最小単位が、素粒子の質量であるわけだ。(下図参照)
┗┻┻┻┻┛ エネルギー(実数)
□□□□□ 素粒子(自然数)
ここでは、そのような転換が起こるか起こらないかは、その場合ごとに波の状態に依存する。だから、その転換はどうしても、一意的には定まらず、確率的に定まるわけだ。
比喩的に言おう。1メートルの高さから、コップに入っている物体を落とす。床にどういう形で届くかは、コップに入っている物体しだいだ。それが油であれば、床にはなめらかな分布の形で届くだろう。それが砂であれば、油の場合とだいたい同じだろう。しかるに、それがピンポン玉であれば、事情は異なる。ピンポン玉であれば、コップには三つぐらいしか入らない。それが床に届くとき、床にはピンポン玉のための枠がいくつかあるが、その中のどの枠に収まるかは、確率的となる。それというのも、ここでは「最小単位に一定の大きさがある」ということが影響するからだ。そして、最初の揺らぎしだいで、ピンポン玉がどの枠に収まるかが、場合ごとに、異なるわけだ。── こういうことが、確率となる。
もう一つ、比喩的に言おう。バラバラのエネルギーの波(ホワイトノイズ)がある。平均的には、単位量の半分(0.5)だが、ときどき、単位量(1.0)を超える大きさの振幅が生じる。そのとき、単位量を超えたことで、エネルギー条件を満たし、何らかのことを実現する。……たとえば、スイッチをONにするとか、アナデジ変換で0から1に転じるとか。……それと同様のことが、「波から粒子に転じる」という形で起こる、と考えるとよい。
かくて、転換の最小単位が存在するということと、事象が確率的になるということは、実質的には同じことである。(揺らぎがあることを前提とすれば。)── ここでは、最小単位があるせいで、波から粒子への転換は、確率の形で発生するようになる。そして、その転換という現象を数理的に記述するためにあるのが、シュレーディンガー方程式だ。
ともあれ、転換のときのエネルギーの最小単位が、素粒子の「質量」なのだ。
逆に言えば、こうだ。質量とは、「宇宙の根源となる素粒子の物理量」のことではない。質量とは、「振動する空間において、波から粒子への転換が起こるときの、最小単位」のことである。つまり、「もともと素粒子というものが存在して、素粒子にはたまたま一定の質量がある」のではなくて、「転換の最小単位としての質量が定まるということと、素粒子が定まるということは、同じことだ」となる。
素粒子を知るということは、波から粒子への転換の、最小単位を知るということだ。だから、素粒子の種類をいくらたくさん知っても、それは、「宇宙の根源を知ること」にはつながらない。宇宙の根源を知るには、素粒子の種類のこと以外に、もっと多くのことを知る必要がある。たとえば、本論で述べたことを、はっきりわきまえる必要がある。それなしに、最小単位の種類ばかりをいくら計測しても、最小単位の一覧表ができるだけであって、宇宙の根源を理解したことにはならない。
【 注釈 】
上記では「粒子のように」という言葉を使った。この言葉は、誤解を招くかもしれないので、注釈しておく。
「粒子のように」という言葉を使ったのは、「本当は粒子ではないが、便宜上、粒子のように扱う」という意味ではない。
ここで否定されているのは、光の「粒子説」である。では、光の「粒子説」とは、何か? それは、「光は一つの粒子である」という説だ。つまり、ド・ブロイ波と同様に、「一つの ◯ が振動しながら移動する」という説だ。
一方、本論は、「多数の ◯ たちが振動することで波が移動する( ◯ は移動しない)」という説だ。これは、「光は一つの粒子である」とは主張せず、「光は粒子の波である」と主張する。
この二つの説は、図で対比的に示される。 ( → 巻末の図 )
( ※ 本論は、「光は一つの粒子である」という説を否定するが、「光が粒子たちの波である」と主張する。だから、光の量子性を否定するわけではない。当然、光電効果などの、「光の量子説」を容認する。本論は、光の「粒子説」は否定するが、光の「量子説」は否定しない。この点、勘違いしないように、注意しよう。)
ここまで、いろいろと述べてきた。で、結局、何が大事なのか?
それは「理論世界」と「現実世界」の区別である。二重スリットの問題も、(後述の)量子テレポーテーションの問題も、しょせんはここに帰結する。そこでは、「観測」ということについて勘違いが起こる。
観測とは、何か? コペンハーゲン解釈では、「観測が量子の状態を決定する」と見なされた。そのことで、次の二つの問題が発生した。
一つは、二重スリットの問題だ。「観測したことで、量子の状態を示す波動関数が急激に収束する」という主張が生じたが、このような主張は、矛盾をもたらす。
もう一つは、(後述の)量子テレポーテーションの問題だ。「観測したことで、一方の量子状態が確定し、同時に、他方の量子状態が確定する」という主張が生じたが、このような主張は、「光速以上の情報伝達」という奇妙な結論をもたらす。
両者では、何が問題なのか? 「観測が量子の状態を決定する」ということだ。本当は、そうではない。観測は、現実の世界を観察するだけであり、あくまで現実の世界のことだ。理論的結論は、理論の世界において得られる結論であり、あくまで理論の世界のことだ。……この両者は、別々の世界のことである。なのに、この両者を混同すると、おかしな結論が出る。
二重スリットの実験では、「現実の世界における観測が、理論の世界の波動関数を決定する」という主張になるので、おかしな話となる。(本当は、現実の世界における観測は、理論の世界の波動関数とは無関係だ。)
量子テレポーテーションの実験では、「現実の世界における観測が、現実の世界における遠くの現実を決定する」というふうに主張するので、おかしな話となる。(本当は、現実の世界における観測は、理論の世界における遠方には影響するが、現実の世界における遠方には影響しない。なお、ここでいう影響とは、現実レベルの物質的な影響ではなくて、推測を左右するだけの心理的な影響だ。)
ともあれ、理論空間と現実空間とを、はっきり区別しよう。そうすれば、観測に関わるたいていのパラドックスは、氷解する。
前項では、「理論世界」と「現実世界」の区別について、強調した。この区別をはっきりさせるために、おもしろい話題を示そう。それは、「誤認」である。
通常、「観測」という用語を使うときには、「観測したときに事実が正しく認識される」と前提されている。しかし、実際には、勘違いが生じて、「正しい認識」のかわりに「誤認」が起こることもある。
例1 :
コインをトスしたあとで、観測して、「裏」と判定した。ところが、実は、観測者のメガネがピンボケで、誤認していた。本当は、「表」であった。……これについて、コペンハーゲン解釈の物理学者は、こう判定した。「観測によって、裏と判明した。表である確率は、50%から0%に収束した」と。しかし、そうだとすると、表である確率が0%であるのに、実際は表(100%に相当)であるから、矛盾。一方、表である確率が 100%だとすると、観測のあとの収束(100%)は、誤認された観測結果(0%)とは逆のことを意味するので、これも矛盾。
例2 :
シュレーディンガーの猫の実験をする。一定時間後に観測すると、猫が倒れているのを観測するので、「猫は死んでいる」と判定する。ただし、猫は倒れているだけであって、本当は生きているのだ。それを誤認するわけだ。……すると、コペンハーゲン解釈の物理学者は、こう判定した。「猫は死んだ。ゆえに、猫の生存確率に相当する波動関数の値が、50%から0%に急激に収束した」と。
ところが、そのあとで、猫がむっくり起きあがって、猫が実は生きていたと判明する。そのとたんに、波動関数の値が、0%から100%に上昇する。
ところが、その後、猫が起きあがったのは、誰かが死体に電気ショックを与えただけで、猫は本当は死んでいた、と判明する。すると今度は、波動関数が100%から0%に変動する。
この際、多くの人々が同時に猫を観測しているとしよう。そして、途中で観測をやめたとしよう。すると、ある人は「猫は死んだ」と思い、ある人は、「猫は生きている」と思う。かくて、波動関数はバラバラの値になる。もはやメチャクチャだ。
例3 :
同様な例は、まだいろいろとある。特に、手品がそうだ。猫が生きていると見える手品や、猫が死んでいると見える手品や、猫がハトに化ける手品や、猫が箱から消失する手品。そういう手品を見ると、観測者が観測したとき、そのたびに、波動関数が、コロコロと変わる。(観測による収束が起こるので。)
さらに、手品師は、こう叫ぶだろう。「観測が事実を決定するのなら、おれは大金持ちだ。客をだまして、お札が増えたと観測させると、実際にお札が増えるのだから。こんなにうまい話はない」と。
以上に、三つの例を示した。馬鹿馬鹿しくて、やってられなくなりそうだ。
はっきり言おう。誤認は誤認だし、観測は観測だし、現実は現実だ。観測されたことはあくまで観測されたことであるにすぎない。観測が事実を決定することなどはありえない。観測と事実とを、はっきりと区別するべきなのだ。そしてまた、観測と理論とを、区別するべきなのだ。
観測とは、理論と現実とを結びつけるための、ただの判断手段にすぎない。その判断手段によって、人は何らかの結論を出す。しかし、その結論が間違っていることもある。また、どっちみち、人がどう結論しようと、現実そのものは左右されない。(たとえば、狂人が「世界は滅んだ」とか何とか、勝手に妄想したことを叫んでいても、それによって現実は左右されない。狂人の言葉を真実だと思うのは、量子論学者だけだ。)
観測とは、理論と現実とを結びつつけるための、弱い紐のようなものだ。その紐が強ければ、理論と現実とはかたく結びつくので、うまく一致する。その紐が弱ければ、理論と現実とはあいまいに結びつくので、誤認も起こる。つまり、一致することもあるし、誤認が起こることもある。ここではとにかく、理論と現実とは別のことだ、と理解するべきだ。なのに、「理論と現実とは常に強く結びつく」と勘違いすると、コペンハーゲン解釈ふうの勘違いを起こす。
もう一度、繰り返して言う。「理論と現実とは別のことだ」と。このことを、深く理解しよう。さもないと、夢想と現実とを混同する狂人の妄想を信じて、自分自身が狂人の仲間となってしまう。
最後に、「観測」の本質を示そう。
「観測とは、事実の状態を測定することだ」
と思っている人が多いようだが、それは、間違いである。なぜなら、測定には、「誤った計測」というものが起こるからだ。(前述の「誤認」のこと。「錯覚」と言い換えてもよい。)
では、正解は? それは、こうだ。
「観測とは、測定すること自体ではなくて、測定に依拠して判断を下すことだ」
ここでは、「測定すること」が大事なのではなくて、「判断すること」が大事なのだ。測定は測定であり、判断は判断だ。測定は現実世界のことだが、判断は人間の頭のなかの世界のことだ。判断は、事実そのものではなくて、事実への認識であって、人間的なものだ。
だから、判断を間違えることもある。ただし、それはそれで、その人だけの問題だ。誰かが判断を間違えたとしても、それで現実が変わるわけではない。誰かが、生きた猫を「死んでいる」と誤認したところで、それで猫が死ぬわけではない。(コペンハーゲン解釈によれば、人が「死んでいる」と誤認すると、本当に猫が死んでしまう、というふうになりがちだが。)
測定は、現実と結びつく。しかし、測定に依拠した判断は、現実そのものとは結びつかない。測定と判断との間は、人間的なものだ。
[ 現実対象 ]━━━━━━[ 測定手段 ]……………[ 人間 ]
測定 判断
測定は客観的だが、判断は主観的だ。この両者は、通常は一致すると見なされるが、食い違うことがあり、それが「誤認」だ。
とすれば、たとえ「誤認」が起こらなくても、測定と判断はしょせんは別物なのである。なのに、この両者を一体化して「観測」と呼ぶと、矛盾が起こる。
「観測」と呼ばれるものの本質は、「測定」自体ではなくて、「判断」である。「測定」は単に「判断」のために依拠するだけだ。
では、「判断」とは、どうすることか? ──それを説明するのが、二重空間モデルだ。
二重空間モデルでは、二つの数学空間を切り替える。それが「判断」の本質だ。最初は、理論に依拠して数学空間を与え、次に、測定に依拠して別の数学空間を与える。
二重空間モデルでは、理論の世界には「波」の数学空間を与え、現実の世界には「粒子」の数学空間を与える。前者では、波動関数が実数で示され、後者では、存在個数が自然数で観測される。
なお、ここでは、一つの現実を示すために、二つの数学空間を用意している。そのことに注意しよう。
特に、測定に依拠する数学空間は、現実そのものではない。現実そのものを扱うことは不可能だ。現実を扱うために、理論とは別の数学空間を用意する、というところに、二重空間モデルの特徴がある。(その数学空間は、現実そのものではなくて、測定と判断に依拠する数学空間だ。)
ともあれ、この二重性のある特徴を、日常的な言葉でわかりやすく説明すると、「理論の世界では波、観測された世界では粒子」というふうになる。
二重空間モデルと使うと、わかりやすいことがある。それは、「量子は波か粒子か?」という質問に、見事に答えることができるのだ。すぐ前に述べたことの繰り返しになるが、こうだ。
「理論の世界では波、観測された世界では粒子」
「一つの数学空間では波、別の数学空間では粒子」
つまり、量子というものは、本質的に、波と粒子との二重性を備えている。そのどちらになるかは、先天的に定まっているのではなくて、人間の認識の方法しだい(理論か観測か)で、どちらかになるわけだ。
なお、これに対しては、次のような反論も生じるだろう。── 従来の物理学でも、こう結論していたぞ、と。すなわち、
「量子そのものが、波であり粒子であるという、二重の性質をもつ」
つまり、
「量子は、本当は粒子なんだけど、波としての性質ももつ」
なるほど、これもこれで、一つの解釈である。しかし、この解釈だと、現実の場合がどうなるかが、判断できない。ある場合を取ったとき、波としての性質を取るのか、粒子としての性質を取るのか、判然としない。── その典型が、二重スリットだ。ここでは、量子は必ず、干渉縞を生じる。一つ一つの電子を発射したときも、干渉縞を生じる。このことは、「波であり、粒子である」という定義からは、結論できない。「波であれば干渉縞を生じるが、粒子であれば干渉縞を生じない」という結論が出るだけであり、干渉縞を生じるかどうかは何とも言えない。
しかし、本稿の理論を使えば、「必ず干渉縞が生じる」と結論できるのだ。なぜなら、空間を伝わるものもあくまで波であり、一つの粒子が移動するわけではないからだ。( ◯ がたくさんあるモデルを参照。)
ここに、本稿の解釈の意義がある。
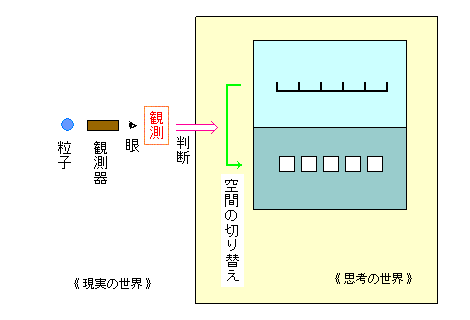
二重空間モデルを、図式化して示そう。というのも、「波から粒子への転換」というのが、少々わかりにくいからだ。それは、人間の観測によって生じるのか? それとも、人間の観測とは無関係に生じるのか? また、実数空間から自然数空間への転換は、人間の意識とどう関係するのか?
そういうことは、次の図式からわかる。

|
解説しよう。
この図式は、時間的に二つの時点で考えるといい。粒子が発生していない時点と、粒子が発生したあとの時点だ。(それぞれ、「時点1」「時点2」と書く。)
【 時点1 】
粒子はまだ発生していない。図の左端の ● はまだ発生していないし、観測されてもいない。
この時点では、何も観測されていないから、人は頭のなかで考えるしかない。すると頭のなかで、波動関数によって、いろいろと考える。それぞれの場所ごとに「発生確率は 0.5 だろう」などと計算する。ただし、現実にどうなるかは、まだわかっていない。
そのまま、じっと観測を続ける。
( ※ 計算する人と観測する人は別であってもいい。たとえば、計算する人は物理学者で、観測する人は子供であってもいい。ただし、その場合、「誤観測」とか「誤伝達」などのケースがまぎれこむので、話は少し複雑になる。)
【 時点2 】
粒子が発生した。図の左端の ● が発生して、観測される。
この時点では、すでに観測されたのだから、それぞれの場所ごとに有無(存在か無か)が判明する。たとえば、 □□□□□ というそれぞれの位置ごとに、 □■□□■ とわかる。そして、そのことを、頭のなかで認識する。(図の右半分の、「思考の世界」で。)
このとき、思考の世界では、「空間の切り替え」が起こる。つまり、「実数の世界から自然数の世界へ」つまり「波の世界から粒子の世界へ」という、空間の切替だ。(そのことを主張するのが、二重空間モデルの趣旨だ。)
ただし、これが起こるのは、物理学者の頭のなかでのことだ。たとえば、子供の場合は、観測しても、このような「空間の切り替え」は起こらない。単に「きれいだなあ」などと眺めるだけである。粒子の存在の有無を位置ごとに確認することもないし、その分布状態を波動関数で予想された分布状態と照合することもない。子供の場合は、観測という行為だけがあり、思考の世界は皆無である。もちろん、「空間の切り替え」も起こらない。当然ながら、コペンハーゲン解釈における「波動関数の収束」なんてことも起こらない。(子供の頭には。)
「空間の切り替え」をもたらすのは、人間の「判断」である。(図を参照。)「判断」が、「観測」に応じて、「空間の切り替え」をもたらす。ここで、「観測」が正しくても、「判断」が間違っていれば、「誤判断」が生じる。間違った形で「空間の切り替え」が起こることもある。とはいえ、その場合も、現実世界の粒子状態そのものが変わるわけではない。コペンハーゲン解釈では、「観測者が、ありもしないものをあると誤認識したら、存在しない粒子が存在することになる」というふうな矛盾を引き起こすが、本論の発想では、現実世界と思考世界とは別々だから、たとえ誤判断が起こっても、現実世界が影響を受けることはない。
まとめて言えば、こうだ。
現実の世界で、何もない 「 」 という状態から、粒子が発生した「 ● 」という状態に変化する。このとき、時点1から時点2へ、時間が経過している。
それに応じて、人は、頭のなかの数学空間を切り替える。波動関数に依拠する数学空間(実数空間)から、観測に依拠する数学空間(自然数空間)に、切り替える。このような切替は、人間の頭のなかでなすことである。現実に依拠するが、現実そのものとは異なるし、現実の世界のことではない。
現実の世界で事象が変われば、それが観測されて判断されるので、人間の思考世界のことも変わるが、ここで起こるのは、「数学空間の切り替え」だけである。つまり、実数空間のなかで、波動関数が急激に変動するわけではない。(コペンハーゲン解釈は正しくない。)
なお、現実の世界で事象が変われば、それが観測されて判断されるので、人間の思考世界のことも変わるだろう。しかし、人間の思考世界のことが変わったからといって、現実の事象が変わるわけではない。たとえば、人間が誤認したからといって、現実の世界が変動するわけではない。また、人間が観測したとか観測しないとか、そういうことによって、現実世界のことが変わるわけでもない。
ただし、粒子が観測されると、時点1の状況から、時点2の状況へと、状況が変化する。推論するしかなかった状況から、すでに観測によって確認された状況へと、状況が変化する。── このことについて、「観測が状況を変化させた」と思い込むと、「観測が現実を左右する」というふうに結論することになる。しかし、それは、勘違いだ。ここでは単に、「状況が変化したから、観測された」だけのことだ。「観測されたから、状況が変化した」のではない。
実際、観測状況としては、いろいろとある。たとえば、目を閉じていたり、観測器が壊れていたり、複数の人が別々の観測精度で観測していたり。……それらの場合、いろいろと異なる観測に応じて、現実が影響を受けていろいろと変動する、ということはない。あるとすれば、矛盾する。二つの対立する観測が一つの同一の現実を決定することになるからだ。(誤認の問題。)
現実の世界と思考の世界は、あくまで別々だ。現実は思考に影響するが、思考は現実に影響しない。もちろん、「意識が現実を決定する」なんていうことはありえない。観測とは、「現実 → 意識」という流れであって、「意識 → 現実」という流れではない。
結論をもう一度繰り返す。「観測されたから、状況が変化した」のではない。「状況が変化したから、その変化が観測された」だけのことだ。
なお、二重スリットの場合の「途中観測」について、付言しておこう。「途中観測」については、前述したとおりだ。つまり、観測が現実に影響したのではなくて、途中観測した場合としない場合とは、別の事象なのである。
ここでは、「途中観測をした」という人間の行為や意識が問題なのではなくて、「途中観測ができたこと」、つまり「波がエネルギーの最小単位を越えて質量をもつ粒子に転じたこと」が、二つの事象を区別している。
要するに、「人間が観測という行為または意識をしているかどうか」が問題なのではなくて、「そこに粒子が実際に出現しているかどうか」が問題なのだ。主観的なことが問題なのではなくて、客観的なことが問題なのだ。……だから、たとえ人間が観測という行為または意識をしなくても、そこに粒子が登場しているならば、観測をした場合と同じ結果になるはずだ。逆に、人間が観測という行為または意識をしていても、そこに粒子が登場しなければ、観測をしていない場合と同じ結果になるはずだ。
わかりやすく言おう。メガネをかけた人が観測するとき、その人のメガネが曇っていれば観測できず、メガネが曇っていなければ観測できる。メガネが曇っているか否かで、観測できるか否かが異なる。……この際、コペンハーゲン解釈では、「メガネが曇っているか否かで、観測できるか否かが変わるから、粒子が存在するか否かも変わる」となる。しかし、本論の見解によれば、意識と現実とは別だから、メガネが曇っているか否かは、粒子が存在するか否かに影響しない。
( ※ このことをいっそう典型的に示したのが、「カシミール効果」の実験だ。)
前項の最後のことから、「観測とは何か」ということに、結論が出る。
観測とは何か? それは、人間または観測器が検出する、という主観的な現象ではない。「波が粒子になる」という客観的な現象だ。では、その本質は? 「複素数波の形であったエネルギーが、質量をもつ形に変わった」(だから観測できるようになった)ということだ。
ここでは、エネルギー自体は同じである。無から有が生じたわけではない。ただし、エネルギーが、見えない形の複素数波から、見える形の物質に転じた。つまり、「観測できる」形に変わった。それがつまり、「観測」の本質だ。
ここでは、発想の転換が必要だ。従来の発想だと、こうなる。
「世界の本質は、存在と無である。存在とは物質のことであり、無とは真空のことだ。無の真空のなかを、確率波という抽象的な(実体のない)波が伝播して、ある場所で急に、確率を高めて、無から物質を誕生させる」
本論の発想だと、こうなる。
「世界の本質は、エネルギーである。ただしそのエネルギーは、観測される形と観測されない形とがある。われわれが物質と見ているのは、無に対する存在ではなくて、観測不可能なものに対する観測可能なものであるにすぎない。同じものが、観測可能なものから観測不可能なものになると、消失したと見なされ、逆に、観測不可能なものから観測可能なものになると、発生したと見なされる。さて。粒子が移動するという現象には、一つの粒子が移動する場合と、多くの粒子が次々と玉突き現象をする場合とがある。電子銃と二重スリットの場合には、後者が起こる。この場合、途中では、観測されるものがいったん観測されないものに転換する。そのせいで、波としての干渉が起こる。これはミクロ的な世界の現象だ。一方、マクロ的な世界ではどうか? たとえば石という一つのかたまりが移動する。この場合には、一つのかたまりが観測不可能なものに転じることはないから、波になることはない。そのせいで、波としての干渉が起こらない。……結局、粒子か波かという問題は、観測可能なもの(物質)であるか観測不可能なもの(複素数波)であるかということに帰着する。マクロの世界の物質は、常に観測可能なかたまりだが、ミクロの世界の粒子は、観測不可能な波に転じることがあるのだ。」
[ 余談 ]【 余談 】
コンプトン効果について、簡単に解説しておこう。
コンプトン効果は、X線が電子にぶつかったときに起こる効果だ。これは、X線がただの電磁波であると仮定するとうまく説明できないが、X線が一定のエネルギーをもつ粒子であると仮定するとうまく説明される。このことから、「光の粒子説」が成立する、というふうに見なされる。
この件は、上記の二重スリットの場合で電子の「波」を考えたのとは違って、光の「波」を考えている。考察する論点が異なっている。
では、光について考えるとして、本論では、コンプトン効果はどう説明されるか? 本論における「波」というのは、「真空中における ◯ たちの波」である。それは「 ◯ という粒子の波」であるから、そこにはもともと粒子性がある。もちろん、光についても、 ◯ という粒子の波で考えられる。
なお、コンプトン散乱を起こすのは、波長の短い電磁波であるX線であるが、そもそも、波長が短ければ、粒子としての性質が強く出るのは当り前だ。
先 に、密集する ◯ たちに一つの ◯ が衝突する図を示したが、この図で考えてみよう。波長が短ければ、 ◯ の衝突後、 ◯ たちの波は、幅広く拡散しないで、狭いビームで直線上を進む。つまり、ただの一次元の玉突きと同然となる。こうなれば、粒子であると見なしてもいいことになる。それだけのことだ。逆に、波長が長ければ、粒子としての性質は強く出ない。 ◯ の衝突後、 ◯ たちの波は、幅広く拡散するからだ。
というわけで、コンプトン散乱の結果を見て、「光には粒子性がある」と結論するのは、早計である。そう言えるのは、波長が短い場合だけだからだ。正確に言うなら、「光には、粒子と波の双方の性質がある。波長が短いほど粒子としての性質が現れ、波長が長いほど波としての性質が現れる」と言うべきだ。コンプトン散乱が示すのは、そのことだけだ。つまり、「コンプトン散乱は、光が粒子であることを示した」という一面的な解釈は正しくない。なぜなら、長い波長の電磁波を使えば、コンプトン散乱は起こらないからだ。
( ※ なお、「光が粒子と波の、二つの性質をもつ」ということについては、従来の解釈と本論の解釈は、異なる意味で考える。……従来の解釈では、粒子とは、光子という一つの粒子のことだ。つまり、一つの ◯ があって、それが波の性質をもつ。一方、本論の解釈では、粒子とは、たくさんの ◯ たちのことだ。つまり、たくさんの ◯ たちがあって、それらがいっせいに振動することで、波が発生する。……この件は、本書の最後のあたりの図でも示してある。 → 該当箇所の図 )
[ 参考 ]
コンプトン効果で電子がはじき飛ばされたあと、その電子はどうなったか? それについては、ウィルソンの霧箱で、写真撮影された。この写真を見ると、光速に近い電子の経路は、直線である。幅広い波ではない。
では、電子は、波ではなく粒子なのか? ウィルソンの霧箱の結果(直線状の軌跡を描くこと)は、本論の解釈(粒子でなく波であること)に矛盾するのか? ……実は、矛盾しない。ウィルソンの霧箱における直線状の軌跡は、気体中の軌跡であって、真空中の軌跡とは異なるから、本論の話とは別のことなのだ。
この件は、次の箇所を参照。( → ウィルソンの霧箱 )
[ 補足 ]
放射線の軌跡を見る方法としては、ウィルソンの霧箱や泡箱がある。前者は、気体中の軌跡を見るもので、後者は、液体中の軌跡を見る。いずれにせよ、真空中の軌跡を見るものではない。
では、なぜ、真空中の軌跡を見ないのか? コンプトン散乱を使えば、X線によって、真空中の軌跡を知ることができるはずなのだ。なのに、なぜ、誰もそうしないのか?
もちろん、それが不可能だからだ。そんなことをやろうとした人は、おそらく、非常にたくさんいただろう。コンプトン散乱の計測装置ならば、多くの大学にあるから、運動する電子の軌跡について計測しようとする研究も、当然たびたび実施されたはずだ。しかるに、その方法では、真空中の軌跡を知ることができなかったのだろう。だから、今日までずっと、霧箱や泡箱を使っている。つまり、真空中の軌跡を直接的に測定するのではなく、気体中や液体中の軌跡を間接的に測定するだけだ。それというのも、真空中の軌跡を直接的に測定することが不可能だからだ。
要するに、霧箱や泡箱なんていうものを使っているという現実が、上記で提案した実験の結果をすでに予告している。つまり、「真空中にX線をかけて、運動中の電子の軌跡を知る」ということは不可能だ、と。そして、その理由は、「真空中を進む電子の軌跡は、直線にはならない」ということだ。換言すれば、「真空中を進む電子は、粒子ではなく波である」ということだ。……そのことが、霧箱や泡箱なんていうものを使うしかないという現実から、明らかに推定できる。
( ※ ガイガー計数管というものもある。これは、コンプトン散乱に似た現象を扱う。ただし、放射線を一つ二つと数えるわけだから、放射線は粒子となっている必要がある。というわけで、計数管の内部は、真空ではなくて、気体が封入された空間となっている。ここでも「真空中ではない」というふうになっている。一方、真空中で電子線を走らせるものとしては、真空管や光電子増倍菅があるが、これらは、真空中を走っている電子を計測するのではなくて、感光面に達したあとの静止した電子を計測する。)結局、こうだ。電子は、走っているときならば真空中でなく気体中か液体中にあるし、真空中であるならば走らずにほぼ静止している。そのいずれかだ。真空中を高速で走っているときの電子を、粒子として測定することはできない。これが現実だ。そして、その理由として、本論は、「真空中を高速で走っているときの電子は、粒子でなく波となっている」と主張する。粒子でないものを粒子として測定することはできないのは、当然なのだ。
( ※ ガイガー計数管とは別の種類の計数管というのも、いろいろと考えられている。比例計数管・電離箱などだ。検知器で得たデータを、コンピュータ処理して、コンピュータ上に軌跡を描く、ということもなされている。ただし、この計数管もまた、調べる対象となる電子などが、真空中ではなくて気体中にある。……ついでに言えば、チェレンコフ光の計数管というのも、真空中でなく液体中を走る放射線の現象を測定する。)
二重スリット実験に戻って言おう。従来の説は、こう主張する。「X線を照射して、電子がどちらのスリットを通ったかを観測すると、経路が一つに決定されてしまう。観測されなければ二つの経路を通ったのに、観測されると一方の経路に決定されてしまう。つまり、観測によって波動関数が収束する。これは電子がX線を受けたことの影響だ」と。……しかし、そんなことはない、と本論は主張する。スリットを通るのが波である限り、波は観測されないのだ。たまたま粒子が観測されることがあるとしたら、それはたまたま波が粒子に転換した場合だけだ。そういうことはほとんどありえない。(ただし、スリットに気体が充満していれば、そこはもはや真空ではないので、そこで波が粒子に転換する。)
氏 名 南堂久史
メール nando@js2.so-net.ne.jp
URL http://hp.vector.co.jp/authors/VA011700/physics/2slits.htm (概要のページ)
[ THE END ]