
シュレーディンガーの猫の核心
by 南堂久史
 シュレーディンガーの猫の核心 by 南堂久史 |
シュレーディンガーの猫の核心を、初心者向けに、ごく簡単に示す。
(核心をざっと理解したあとで、表紙ページに記した各ページを読むとよい。)
(ただし、下記の ★ をあらかじめ読んでおくといいだろう。)
※ 「量子力学のミクロとマクロ」 という注釈ページを追加した。( 2006-06-30 )
※ 「「シュレーディンガーの猫」の破綻」 ★ を追加した。( 2007-09-02 )
【 エピソード1 】
男が女に求婚した。
「きみが好きだ。結婚してくれ」
しかし女は迷った。
「困ったなあ。あなたのこと、半分だけ好きなの。半分だけなら、結婚してもいいわ」
「半分結婚なんて、ありえないよ。結婚するか、結婚しないか、どっちかだ。どっちにするか、とにかく決めてくれ」
「そんなこと言っても、半分好きなんだから、しょうがないでしょ。決められないわよ」
白黒で決められないものを、白と黒のどちらかに無理に決めようとすると、ジレンマが起こる。……これが実は、「シュレーディンガーの猫」の本質だ。
| (1) 量子は「離散的」である。 | (1,2,3,……) |
| (2) 量子は「粒子」である。 | ○ ○ ○ ○ |
| (3) 離散的な粒子には、中間的な個数はありえない。 | 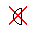 |
| (4) 量子力学で(波動関数によって)与えられる値は、存在確率であり、0と1の間の中間値である。 | Ψ= 0.5 |
| (5) 個数は中間的な値ではありえないのに、存在確率が中間的な値である。 | 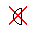 かつ Ψ= 0.5 かつ Ψ= 0.5 |
| (6) では、両者はどういう関係にあるか? この関係は「重ね合わせ」という解釈で説明できる。それは、「二つの状態が同時に成立する」という意味だ。(コペンハーゲン解釈) | 0.5 = 1 & 0 ● = ○ & ● (同時成立) |
| (7) ミクロの状態とマクロの状態を、うまく対応するように、結びつけることができるはずだ。(これが「シュレーディンガーの猫」の実験システム) | 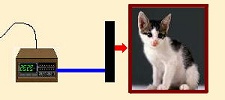 ミクロ = マクロ |
| (8) ミクロにおいて「二つの状態が同時に成立する」のであれば、マクロにおいても「二つの状態が同時に成立する」というふうになるはずだ。 | ミクロの同時成立 = マクロの同時成立 |
| (9) そうとすれば、マクロの世界では、「『生』という状態と『死』という状態が同時に成立する」というふうになるはずだ。 | [ Ψは0.5 ]= [猫は ● ] (ミクロで) (マクロで) |
| (10) しかし、「『生』という状態と『死』という状態が同時に成立する」ということは、ありえない。一匹の猫は、「生きていて、かつ、死んでいる」ということは、ありえない。ゆえに、矛盾。 | × [ 猫は ● ] × [ 猫は ○ かつ ● ] (マクロでは、同時成立はありえない) |




【 解説 】
0.5 という中間的な値を説明したい。
ここで、粒子説を前提とすると、「灰色」または「白と黒の重ね合わせ」という発想が生じる。しかしその発想には無理がある。その無理が、シュレーディンガーの猫のパラドックスだ。
そこで、粒子説を捨てて、「波」であると理解すればよい。離散的な粒子については、0.5 という中間的な値を取ると考えると、不自然な結論が生じる。だが、連続的な波については、0.5 という中間的な値を取ると考えれば、自然な結論が出る。(だから、運動する粒子については、「離散的な粒子」と考えずに、「連続的な波」と考えればよい。……静止した粒子でなくて、運動する量子については。)
量子は波であると見なされるべきだ。では、量子が波であることは、どういうふうに説明されるべきか? そのためのモデルを使えばいい。ここで登場するのが、「粒子の波」という形のモデルである。つまり、量子が「粒子であると同時に波でもある」ということを示すための、具体的なモデルだ。このモデルは、「本質的には粒子であるが波の性質ももつ」というド・ブロイ波のモデルとはまったく異なるモデルだ。
( ※ ここでは、通常の量子力学の数式が否定されているわけではない。否定されているのは、ド・ブロイ波のモデルだけである。混同しないように注意。)
 かつ かつ  |
(1) 「粒子」説 ○ と ● とが「重ね合わせ」の状態にある。 |
|
●●● ● ●●●●●●●● ●●●●●●●●●● ●●● ●●●●●●●● ●●●● ● ●●●●●●●●●●● |
(2) 「砕かれた微細な粒子」説 微細な ○ と ● が無数に混合する。 (それぞれの大きさは無限小。無限小 × 無限個 = 1個) |
 |
(3) 「粒子の波」説 波が伝わるとき、それぞれの量子が振動する。 ここで、「振動」とは、 ○ と ● とが交替することである。(「粒子反粒子振動」という概念に近い。) (比喩的に言えば、「人の波」が伝わるとき、それぞれの人が立ったり座ったりするのが「振動」に相当する。) |
紫 = 赤点 と 青点 の「散在」 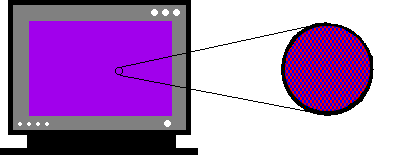
|
紫 = 赤状態 と 青状態 の「重ね合わせ」  |
●●●●●●●●●●●●●●
●●●●●●●●●●●●●●
【 エピソード2 】
女に言われたあとで、男が決めつけた。
「半分好きだということは、好きな状態と好きでない状態とが、重ね合わせになっているんだ」
しかし女はいぶかった。
「重ね合わせ? それ、どういうこと?」
「体と体の重ね合わせじゃないよ」
「ふざけないで」
「いてっ。ぶつなよ。……つまりね、心と心の重ね合わせのことさ」
「あなたとあたしの?」
「じゃなくてね。きみ自身の心と心」
「どういうこと?」
「きみのなかに、二つの心がある。一つの心は好きだと言っているが、もう一つの心は好きでないと言っている。きみのなかに、二つの心が共存しているんだよ」
女は呆れた。
「あなた、馬鹿じゃないの? 心の平均値の計算なんかしないで。あのね。半分好きだということは、好きと嫌いがいっしょにあるということじゃないわよ」
「じゃ、何なのさ?」
「どちらでもあるんじゃなくて、どちらでもないのよ」
「え? 半分好きって、そういう意味かい?」
「当り前でしょ」
「僕のこと、好きでも嫌いでもない、ってこと?」
「まあね」
「そうかなあ」
「でも、そうなの」と断言した。「まだわからないの? あなたって、女心がちっともわからないのね」
「だって、物理学者だから……」
「ふん。こんなことじゃ、物理のことだって、どれだけ知っているか、怪しいもんだわ。あたしの方がよく知っているかもよ」
そう言われてみると、男は何だかそんな気がしてきた。
※ エピソードの続きは、「重ね合わせ」とは何か? のページで。
( 初心者向けの解説は、これで終わり。より詳しい話は、「表紙」のページから、もっと先のページを読んでほしい。)
【 オマケ 】
※ いわずもがなのことだが、このサイトは個人サイトである。
もちろん、内容も個人ホームページの内容である。ここは決して
日本物理学会のサイトではないし、百科事典のサイトでもない。
本サイトに掲載された文章は、すべて筆者個人の見解である。
勝手に勘違いして、「公的サイトでもないのに、公的サイトのフリ
をしているぞ」と怒り狂う人もいるが、この点、誤解なきように。
※ なお、誤解を避けるために、「 …… であると筆者は思う」という
文章を、いちいち書き足すべきかもしれない。しかし、そうすると、
それが数百箇所も追加されて、煩雑になりすぎて、読みにくくなる。
だからいちいち「 …… と筆者は思う」というふうには書かない。
こんなことは、常識的なことなのだから、勝手に怒らないでほしい。
(ついでに言えば、主流派の解釈も、「 …… と我らは思う」という
文句は付いていない。)
※ このページは、初心者向けではあるが、「イロハのイ」も知らない人
向けではない。シュレーディンガーの猫のイロハぐらいは知っている人
向けである。「イロハのイ」も知らない人は、別サイトで、イロハを勉強
してほしい。「ど素人向けにはコペンハーゲン解釈の説明が不足だ」と
怒る人もいるが、本サイトはど素人向けではない。怒らないでほしい。
※ 「コペンハーゲン解釈こそ正統的な解釈だ。それ以外の解釈は不要だ」
と思った末に、このサイトに書いてある文書の話を読んで、「トンデモだ」
と思う人がけっこういる。
実を言うと、コペンハーゲン解釈は正統的な解釈というわけではなく、
単に現状では比較的には支持者が多い、というだけのことにすぎない。
もちろん、定説ではない。絶対的に正しいと合意されたわけでもない。
※ 本サイトで述べていることは、「何通りかの解釈がある」ということと、
「そのうちの最後の解釈が、最も正しいだろう」という見解である。
(これに対して、「新たな解釈が提出されること自体がけしからん」と
怒り狂う人もいる。仮説や新説というものを拒否したがるわけだ。)
※ 以上のことがわからずに、「コペンハーゲン解釈こそ正統的な解釈だ」
と思い込んでいる人のために、下記の文書を用意した。疑問や不満を
感じた人は、下記の文書を読むといいだろう。
(ファインマンの発想を素直に理解できる人なら、いちいちこれを読む
必要はないが。)
→ 「核心」の誤解を避けるために
[ THE END ]