 or
or 
停止中 = 粒子 or 反粒子

回転中 = 粒子 or 反粒子 or 仮想粒子
本サイトで示した量子論の記述で書き落とした周辺的な話題を扱う。
《 基本的な話題 》
モデルの重要性
重ね合わせ
波動関数の収束
仮想粒子
運動中の粒子
トンネル効果
物質中の電子
場の量子論との関係
* * * * * * *
《 些末な話題 》
エーテルの用語法
負のエネルギー
3の神秘
量子コンピュータ
量子テレポーテーション
ベル不等式関係
EPRパラドックスと観測の問題
たいていの学者が数式だけであれこれと表現するときに、ファインマンは「あなたの考えを、図で示してくれ」と言った。すると、たいていの人は、途方に暮れてしまった。自分の考えを、数式で表現することはできても、図で表現することはできないのだ。実は、数式というのは、「物事の細かな部分を精密に示す」という役割だけがある。そして、物事の骨格となる肝心の部分は、モデルが示すのだ。
図で表現するということは、物事の本質を示すということだ。ファインマンは、そのことの重要性を理解していたから、「図で示してくれ」と言ったのだ。そして、たいていの人は、物事の本質を理解していないから、「図で示してくれ」と言われたとき、途方に暮れてしまうのだ。
( ※ 「観測のためには光を当てるので、光を当てたことが影響する」という解釈もあるが、妥当ではない。「観測するか否か」では、「光を当てたか否か」が問題なのではなく、「光を当てたあとで人間が見るか見ないか」が問題となる。ずっと光を当てっぱなしで、そのあとで、見たか見ないかが問題なのだ。)
( ※ 超球理論の立場で言えば、電子に光を当てることはほとんど影響しない。光を当てたからといって、波が粒子に変換されるわけではない。一方、光を当てなくても、真空中で粒子が発生することはある。場の量子論から当然の帰結だ。)
( ※ 要するに、「観測が現実に影響する」というのは、どう考えてもおかしいのだ。)
《 従来の考え方 》
現実 理論
[ 存在する/存在しない ] [ 存在する/存在しない/仮想粒子 ]
( ※ 従来の考え方では、現実と理論の食い違いが生じる。)
( ※ それは、幽霊や悪魔を信じるような、非科学的な立場である。)
《 超球理論 》
現実 & 理論
[ 静止(実在粒子)/回転(仮想粒子) ]
( ※ 超球理論では、現実と理論の食い違いが生じない。)
( ※ 超球理論では、「何も存在しない真空」というものは、ない。)
( ※ 超球理論では、「存在する」という言葉はあいまいなので使わない。
かわりに、「静止する」という言葉を使う。その反対概念は「回転する」
だが、それは決して「何も存在しないこと」ではない。)
 or or  | 停止中 = 粒子 or 反粒子 | ||
 | 回転中 = 粒子 or 反粒子 or 仮想粒子 |

高速の場合は、始点と終点との距離は長くて、その長い距離を一挙に波が進む。たとえば、2メートルの距離を一挙に波が進む。その速度はとても速い。
・ 高速 …… 玉突きモデルで、始点と終点との距離は長い。
○ → ○○○○○○○○○○○○○○○○○ → ○
・ 低速 …… 玉突きモデルで、始点と終点との距離は短い。
○ → ○○ → ○
・ 静止 …… 一つの超球のまま。(波が発生しない)
○
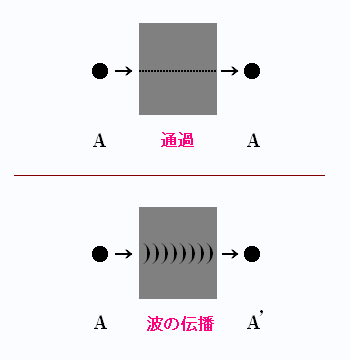 超球理論に従えば、トンネル効果は不思議でも何でもない。「物質中を波が伝わること」と言い換えることができる。右の図を参照。
超球理論に従えば、トンネル効果は不思議でも何でもない。「物質中を波が伝わること」と言い換えることができる。右の図を参照。
|
【 参考 】
ついでに、もう少し細かく考えよう。(特に読まなくてもよい。)
金属中を電位差が伝わる速度は、光速と同じぐらいか?
実は、光速よりは、かなり遅いはずだ。実際、実験結果を見ても、トンネル効果素子に比べて、普通の半導体素子はかなり速度が遅い。では、そのわけは?
超球理論に従えば、たぶん、こうだろう。
「トンネル効果素子では、超球の波が複素数空間を伝わるが、普通の半導体素子では、電子の波が実数空間を伝わる。複素数空間の超球は質量がないが、実数空間の電子は質量がある。後者の方が重い。どちらも玉突きモデルで波が伝わるが、質量のある電子の方が、(玉突きモデルで)波の伝わる速度が遅い。」
◯ → ◯◯◯◯◯◯◯◯◯◯ → ◯
この図で、 ◯ が質量という抵抗をもつと、振動(=波)の伝わる速度が遅くなる。比喩的に言えば、きれいな金属球なら、(玉突きの)波の伝わる速度は速い。金属球にゴミのようなものがくっついていると、(玉突きの)波の伝わる速度は遅い。
|
|
|
|

|
|
|
なお、これと似たことは、前述のトンネル効果でも説明した。
【 たとえ話 】
比喩的に言おう。レンタカー会社からカローラを借りる。ニューヨーク東で借りて、カリフォルニアで返す。さらに七日後に、カリフォルニアで借りて、ニューヨーク西で返す。
(前半) NY 東 ──────────→ カリフォルニア
(後半) NY 西 ←────────── カリフォルニア
前半では、カローラを借りて、カローラを返した。
後半でも、カローラを借りて、カローラを返した。
このすべてを通して、カローラは同じ物である必要はない。前半のカローラと、後半のカローラは、違うカローラであってもいい。カローラは、NY東 から NY西 へと移動したように見えるが、それは見かけ上のことだ。(本当のカローラは、NYとカリフォルニアの間で移動している。)
要するに、レンタカー会社のレンタカーは、たがいに区別する必要のない物なので、一つの物が移動したように見える。(別々の物による現象だとは見えない。)
|
題 名 細々とした周辺的な問題
著者名 南堂久史
URL http://hp.vector.co.jp/authors/VA011700/physics/trivial.htm (本文書)
http://hp.vector.co.jp/authors/VA011700/physics/quantum.htm (表紙)