球 対 称 星
< 目次へ >
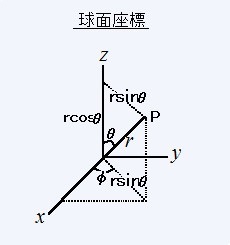 デカルト座標系と球面座標系との間には次の関係がある。
デカルト座標系と球面座標系との間には次の関係がある。r=(X2+Y2+Z2)1/2 , θ=tan-1((X2+Y2)1/2/Z) , φ=tan-1(Y/X)
X=rsinθcosφ , Y=rsinθsinφ , Z=rcosθ
時間tは両方の系とも同じである。 この球面座標系での線要素は
◆ ds2=ーdt2+dr2+r2(dθ2+sin2θdφ2) ・・・・・ (1) である。これを基に強い重力場でのメトリックを求める。式(1)の導出法は付録1:球面座標系での線要素を参照
dl2=r2(dθ2+sin2θdφ2)=r2dΩ2 で表される二次元球面の上に対象となる時空の各点が存在しなければならない。従ってメトリックのθ成分gθθは
gθθ=r2 , φ成分gφφは gφφ=r2sin2θ である。このような球では円周の長さは2πrで、面積は4πrである。
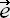 r・
r・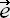 θ=0 ,
θ=0 , 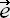 r・
r・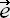 φ=0が成り立ち、メトリックの定義により
φ=0が成り立ち、メトリックの定義によりgrθ=gr'θ'=0 , grφ=gr'φ'=0 又は空間座標の変換によっても線要素の式は不変である。式で表すと
(t,r,θ,φ)→(t,ーr,θ,φ) と座標変換してもメトリックは変わらないという条件により、(3) と同じ方法で
grθ=gr'θ'=0 , grφ=gr'φ'=0 , gθφ=gθ'φ'=0 を導く事が出きる。
(ⅱ)時間の反転(t→-t)に対して幾何学が変化しない事。これは状況を撮影したフィルムを逆回ししても同じに見えるという意味である。
g0'i'=Λ00'Λii'g0i=ーg0i
gi'i'=(Λii')2gii=gii
幾何学は不変なので g0'i'=g0i これと、上の第二式よりg0'i'=g0i=0となる。
以上により、静的で球対称的な星のメトリックは
◆ ds2=ーe2φdt2+e2Λdr2+r2dΩ2・・・・・ (2)
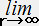 φ(r)=
φ(r)=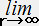 Λ(r)=0 → e2φ=e2Λ=1
Λ(r)=0 → e2φ=e2Λ=1
①メトリックの逆行列及び微分を計算。
②クリストッフェル記号を計算。
③リーマン曲率を計算。
④リッチテンソル及びリッチスカラーを計算。
⑤アインシュタインテンソルを計算。 この計算の過程は、既に「曲った時空 付録3:曲率に関する情報の実例の(4)」で計算しているのでそこを参照。この結果、球対称星でのアインシュタインテンソルは次の様になる。
◆ Gtt =
 (rーre-2Λ)・・・・・ (3)
(rーre-2Λ)・・・・・ (3)◆ Grr = ーe2Λ/r2+1/r2+2φ'/r・・・・・ (4)
◆ Gθθ = r2e-2Λ(φ''+(φ')2-φ'Λ'+φ'/ rーΛ'/r)・・・・・ (5)
◆ Gφφ = sin2θGθθ・・・・・ (6)
局所慣性系から一般の座標系(=非局所慣性系)への座標変換行列をΛαα' とする。(プライムの付いている方が局所慣性系)
gαβ=Λαα'Λββ'ηα'β' , g00=(Λ00')2η0'0' 従って
Λ00'=e-φ ( ∵ g00=-e-2φ ,η0'0'=-1 だから )
 のゼロでない成分はただ一つ U0 である。MCR系(=局所慣性系)ではこの成分は(1,0,0,0)である。この成分を先に求めた座標変換行列Λで一般の座標系(=非局所慣性系)へ座標変換すると、(e-φ,0,0,0)になる。完全流体の、一般座標系でのストレスーエネルギーテンソルは
Tαβ = (ρ+P)UαUβ+Pgαβ
のゼロでない成分はただ一つ U0 である。MCR系(=局所慣性系)ではこの成分は(1,0,0,0)である。この成分を先に求めた座標変換行列Λで一般の座標系(=非局所慣性系)へ座標変換すると、(e-φ,0,0,0)になる。完全流体の、一般座標系でのストレスーエネルギーテンソルは
Tαβ = (ρ+P)UαUβ+Pgαβであった。この式からT00,T11,T22 ,T33を求めると (他の成分はゼロ) T00=ρe-2φ , T11=Pe-2Λ , T22=P/r2 , T33=P/r2sin2θ アインシュタインテンソルの添字の位置が下付けなので、Tも下付けにする。
Tαβ=gαμgβνTμν μ≠ν なら Tμν=0 だから μ=ν だけを計算すればよい。Tαβ=gαμgβμTμμ
α≠μ なら gαμ=0,β≠μ なら gβμ=0。従って α=β=μ だけを計算すればよい。Tαα=(gαα)2Tαα ◆ T00=(-e2φ)2ρe-2φ=ρe2φ ・・・・・ (7)
◆ T11=(e2Λ)2Pe-2Λ=Pe2Λ ・・・・・ (8)
◆ T22=(r2)2(P/r2)=Pr2 ・・・・・ (9)
◆ T33=(r2sin2θ)2(P/r2sin2θ)=Pr2sin2θ=sin2θT22 ・・・・・ (10)
Tαβ;β=Tαβ,β+ΓαμβT μβ+ΓβμβTαμ=0 である。これはフリーな添字αの各値に対しての四つの式である。α=0,2,3に対しては恒等的にゼロになる。(各項がゼロか又は項同士が打ち消し合ってゼロになる)
α=1に対しては対称性から恒等的にはゼロにならない。それを計算すると ( クリストッフェル記号Γの計算は「曲った時空 付録3:曲率に関する情報の実例の(4)」を参照 ) (ρ+P)φ'+P'=0 即ち
◆ (ρ+P)
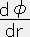 = ー
= ー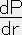 ・・・・・ (11)
・・・・・ (11)
◆ m(r)=
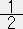 r(1-e-2Λ) , (e2Λ=
r(1-e-2Λ) , (e2Λ=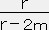 ) ・・・・・ (12)
式(3)と式(7)と式(12)からアインシュタイン方程式の(0,0)成分が求められる。
) ・・・・・ (12)
式(3)と式(7)と式(12)からアインシュタイン方程式の(0,0)成分が求められる。G00=
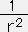 e2φ
e2φ [r(1-e-2Λ)]=
[r(1-e-2Λ)]=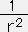 e2φ
e2φ [2m(r)]=8πT00=8πρe2φ
∴
[2m(r)]=8πT00=8πρe2φ
∴ 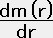 =4πr2ρ ・・・・・ (13)
となる。これはm(r)が半径rの球の質量だとするニュートン的方程式と同じ形である。
=4πr2ρ ・・・・・ (13)
となる。これはm(r)が半径rの球の質量だとするニュートン的方程式と同じ形である。式(4)と式(8)から(r,r)成分の方程式は
Grr=-
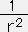 e2Λ
e2Λ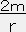 +
+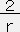 φ'=8πTrr=8πPe2Λ →
φ'=8πTrr=8πPe2Λ → 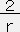 φ'=e2Λ(
φ'=e2Λ(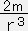 +8πP)
式(12)から e2Λ=
+8πP)
式(12)から e2Λ=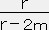 なので、
なので、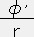 =
= 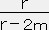 (
(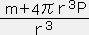 )
∴
)
∴ 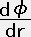 =
=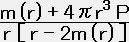 ・・・・・ (14)
・・・・・ (14)
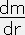 = 0 ,
= 0 , 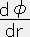 =
= 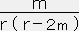 上の二つの微分方程式の解は
上の二つの微分方程式の解はm(r) = M = 一定
 e2Λ =
e2Λ = 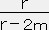 =
= 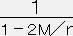
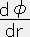 =
= 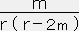 =
= 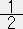 (
( 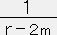 ー
ー  ) 両辺を積分して
2φ=log(r-2m)-log r=log
) 両辺を積分して
2φ=log(r-2m)-log r=log 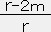
∴ e2φ=1-
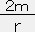 =1-
=1-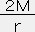 となる。この外部のメトリックはシュワルツシルト・メトリックと呼ばれる。
となる。この外部のメトリックはシュワルツシルト・メトリックと呼ばれる。◆ ds2=ー ( 1-
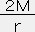 )dt2+(
)dt2+( 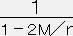 )dr2+r2dΩ2・・・・・ (15)
これが球対称星の外部時空での線要素及びメトリックである。rが十分大きい時には
)dr2+r2dΩ2・・・・・ (15)
これが球対称星の外部時空での線要素及びメトリックである。rが十分大きい時にはds2
 ー ( 1-
ー ( 1-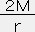 )dt2+( 1+
)dt2+( 1+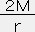 )dr2+r2dΩ2
【シュワルツシルトの半径】
)dr2+r2dΩ2
【シュワルツシルトの半径】ds2=g00dt2+2g0rdtdr+grrdr2+r2dΩ2
◆
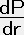 =ー
=ー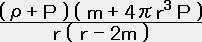 ・・・・・ (16)
これをオッペンハイマー-ヴォルコフ(O-V)方程式という。
(1)星の中心と表面での値
・・・・・ (16)
これをオッペンハイマー-ヴォルコフ(O-V)方程式という。
(1)星の中心と表面での値星の表面は外部時空と連続的につながらなければならないから、星の表面では P=ρ=0 である。
半径をRとすると m=R になる。
内部では grr=(1-2m(r)/r)-1 で、外部では grr=(1-2M/r)-1 である。連続性から星の質量Mは
M=m(R) で定義されることが明らかである。Mが分かると、星の外部での g00 が定まり、星の表面での g00 は
g00(r=R)=ー(1-2M/R) が得られる。
普通の星の場合には 2m(r) < r が常に成り立つ。
◆
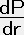 =ー
=ー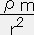 ・・・・・ (17)
と簡単化される。これがニュートン的な星の平衡状態の方程式である。相対論的な圧力勾配はニュートン的な場合に比べて急激である事が分かる。言い換えれば流体を静止させるためには一般相対論では重力がより強い力でなければならない。
・・・・・ (17)
と簡単化される。これがニュートン的な星の平衡状態の方程式である。相対論的な圧力勾配はニュートン的な場合に比べて急激である事が分かる。言い換えれば流体を静止させるためには一般相対論では重力がより強い力でなければならない。白色矮星までの密度の星については、(16)の式の代わりに(17)の式を用い、中性子星のような高密度の星については式(16)を用いる。
◆ m(r)=4πr3ρ/3 , r ≦ R ・・・・・ (18) となる。Rは星の半径で、未だ決まっていない。Rの外側では密度がゼロなので、m(r)は一定となる。grrの連続性からm(r)がRで連続でなくてはならない。従って
◆ m(r)=4πR3ρ/3=M , r ≧ R ・・・・・ (19) Mは星の質量で、シュワルツシルト質量という。式(18)のmを式(16)に代入して
◆
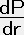 =
=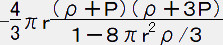 ・・・・・ (20)
上の微分方程式は変数P、rに関しての変数分離形の形であるから、任意の中心圧力Pcを使って容易に積分出来て、
・・・・・ (20)
上の微分方程式は変数P、rに関しての変数分離形の形であるから、任意の中心圧力Pcを使って容易に積分出来て、 ◆
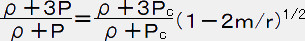 ・・・・・ (21)
星の表面の時、r=R,m(R)=4πR3ρ/3,P=0だから左辺は1になって
・・・・・ (21)
星の表面の時、r=R,m(R)=4πR3ρ/3,P=0だから左辺は1になって◆ R2=
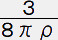 [1-(ρ+Pc)2/(ρ+3Pc)2] ・・・・・ (22)
[1-(ρ+Pc)2/(ρ+3Pc)2] ・・・・・ (22) ◆ Pc=ρ[1-(1-2M/R)1/2]/[3(1-2M/R)1/2-1] ・・・・・ (23) 上の式を使って(18)のPcを置き換えると
◆
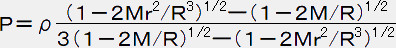 ・・・・・ (24)
式(11)からφ=-log(ρ+P)+C(Cは積分定数)
星の表面ではP=0だから、φ=-log(ρ)+C
・・・・・ (24)
式(11)からφ=-log(ρ+P)+C(Cは積分定数)
星の表面ではP=0だから、φ=-log(ρ)+C又g00(r=R)=ー(1-2M/R)=-e2φより、積分定数Cが求まる。これらと式(11)のPより
◆ eφ=
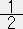 [3(1-2M/R)1/2-(1-2Mr2/R3)1/2] ・・・・・ (25)
[3(1-2M/R)1/2-(1-2Mr2/R3)1/2] ・・・・・ (25)式(12)より e2Λ =
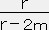 = (1-8πr2ρ/3)-1 だから、星の内部での線要素 ds2は
= (1-8πr2ρ/3)-1 だから、星の内部での線要素 ds2はds2=-
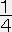 [3(1-2M/R)1/2-(1-2Mr2/R3)1/2]2dt2+(1-8πr2ρ/3)-1dr2+r2dΩ2
以上の求めた式を使った具体例は、
付録5:シュワルツシルトの内部解(密度一定)を参照
[3(1-2M/R)1/2-(1-2Mr2/R3)1/2]2dt2+(1-8πr2ρ/3)-1dr2+r2dΩ2
以上の求めた式を使った具体例は、
付録5:シュワルツシルトの内部解(密度一定)を参照【ブハダールの定理】
上のPcを求める式に於いて、M/R→4/9の時、Pc→∞になる。従って半径が(9/4)Mより小さい
一様密度の星は存在しない。そのような星を静的な状態に支えるには無限大の圧力が必要になるためである。
この事は任意の星のモデルについてもいえて、ブハダールの定理として知られている。
(2)ブハダールの内部解
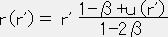 また次の関数が定義される。(付録4:ポリトロープ参照)
また次の関数が定義される。(付録4:ポリトロープ参照)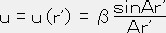 ,
, 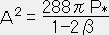 (βは任意の定数)
Ar'≦πの時、ブハダールの解は次の様になる。
(βは任意の定数)
Ar'≦πの時、ブハダールの解は次の様になる。e2φ=(1-2β)(1-βーu)(1-β+u)-1
e2Λ=(1-2β)(1-β+u)(1-βーu)-1(1-β+βcosAr')-2
P=A2(1-2β)u2[8π(1-β+u)2]-1
ρ=2A2(1-2β)u(1-β-3u/2)[8π(1-β+u)2]-1
上の式のPとρから P/ρ=
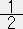 u(1-β-3u/2)-1
星の中心ではr=0で、
u(1-β-3u/2)-1
星の中心ではr=0で、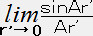 =1 → u=βなので
=1 → u=βなのでPc/ρc=β(2-5β)-1
星の表面について考える。星の表面ではρ=P=u=0。つまりr'=π/A=R'なので
e2φ=e2Λ=(1-2β)
R=r(R')=π(1-β)(1-2β)-1A-1
星の質量Mは 1-2β=1-2M/R から M=βRなので

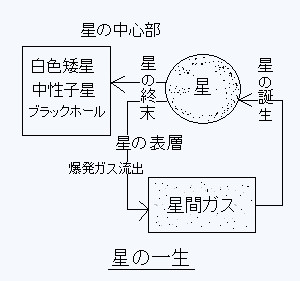 白色矮星、中性子星、ブラックホールがどのように形づくられるかを知るには星のライフサイクルを理解しておかねばならない。星は星間ガスが重力で凝集し、核融合反応が始まり高温になって輝き始める。核融合反応によってヘリウム、炭素、酸素・・・鉄等の元素が段階的に次々作られていく。星が燃え尽き、終末になると表層の物質は爆発又は流出によって星間ガスに戻っていく。星の中心部分は白色矮星、中性子星、ブラックホール等といった非常に高密度で輝きのない天体へと変わっていく。
白色矮星、中性子星、ブラックホールがどのように形づくられるかを知るには星のライフサイクルを理解しておかねばならない。星は星間ガスが重力で凝集し、核融合反応が始まり高温になって輝き始める。核融合反応によってヘリウム、炭素、酸素・・・鉄等の元素が段階的に次々作られていく。星が燃え尽き、終末になると表層の物質は爆発又は流出によって星間ガスに戻っていく。星の中心部分は白色矮星、中性子星、ブラックホール等といった非常に高密度で輝きのない天体へと変わっていく。
(1)星の誕生
主系列星は水素からヘリウムへの核融合の時で、重力により縮まろうとする力と核融合反応で発生する熱によって膨張しようとする気体の圧力が釣り合う安定した状態である。星はその一生の大部分の時間を主系列時代で過ごす。従って宇宙を見ると主系列星の星が圧倒的に多い。重い星は核反応が激しく一生が短く、軽い星ほど寿命が長い。
【主系列星を表面温度で分類】
|
・ 白色矮星
白色矮星を構成する物質はヘリウム、炭素、酸素などである。平均密度は1立方センチメートルあたり1.4トンである。代表的な白色矮星としてシリウス伴星(シリウスB)がある。
-----------------------------
* 水素の原子核を直径1mのボールとし東京駅に置く。ボーアの原子模型では、電子は100キロメートル
先の沼津、日光、銚子辺りを回る事になる。原子の中はスカスカ、すき間だらけである。
中性子星を構成する物質は文字通り中性子で、巨大な原子核が天空に浮遊している様な星である。平均密度は1立方センチメートルあたり10億トンにもなる。中性子星自身は可視光線を発しないため、パルサーとして1967年に発見された。
1970年に入り最初のブラックホール候補、はくちょう座X-1が発見された。ブラックホールは非常に強い重力の為、時空が著しく歪められ、光さえも脱出出来ないので、直接観測する事が出来ない。しかし他の天体との相互作用により(X線を発する)、間接的にその存在が推定される。はくちょう座X-1からX線が観測され、そばにブラックホールがあると断定された。
△P△X=h が成り立つ(hはプランク定数)。△Xを一辺とする微小な立方体の体積を△Vとすると、 △X=△V1/3 だから
△P=h△V-1/3 が成り立つ。△Xが小さくなると、△Pが大きくなり、それにつれPも大きくなる。これが量子力学的圧力(=フェルミ縮退圧、又は単に縮退圧)の源である。核融合反応が活発であった星は、その膨張圧力で星の重力を支えていたが、核融合反応が終了した星は温度を下げながら収縮に向かう。そして重力と縮退圧が釣り合う所まで温度を下げ収縮する。
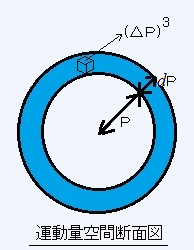 電子の運動量がPとP+dpの間にある時、運動量空間では、球の表面積は4πP2、殻の厚みはdpだから、体積は4πP2dpになる。フェルミ粒子はパウリの排他原理により、複数の電子が同一の状態(例えばエネルギーの一番低い状態)を取る事が出来ないので、又恒星が球状なので運動量空間も球状になる。
4πP2dpを0からPfまで積分した球殻をフェルミ球、最大の運動量Pf(=フェルミ球の半径)をフェルミ運動量、その時のエネルギーをフェルミエネルギーという。
電子が一辺の長さ1x10-11mの直方体の狭い空間に閉じ込められた時(原子の直径は1x10-10m)の運動量は 6.6x10-23Kg・m/sになる。電子の速度は7.25x107 m/sになる。(光の速さは3x108m/s)。フェルミ運動量は電子の運動量より少し大きい値になる。付録6:フェルミ縮退した気体の諸量の計算を参照
電子の運動量がPとP+dpの間にある時、運動量空間では、球の表面積は4πP2、殻の厚みはdpだから、体積は4πP2dpになる。フェルミ粒子はパウリの排他原理により、複数の電子が同一の状態(例えばエネルギーの一番低い状態)を取る事が出来ないので、又恒星が球状なので運動量空間も球状になる。
4πP2dpを0からPfまで積分した球殻をフェルミ球、最大の運動量Pf(=フェルミ球の半径)をフェルミ運動量、その時のエネルギーをフェルミエネルギーという。
電子が一辺の長さ1x10-11mの直方体の狭い空間に閉じ込められた時(原子の直径は1x10-10m)の運動量は 6.6x10-23Kg・m/sになる。電子の速度は7.25x107 m/sになる。(光の速さは3x108m/s)。フェルミ運動量は電子の運動量より少し大きい値になる。付録6:フェルミ縮退した気体の諸量の計算を参照
体積4πP2dpの領域に含まれる、体積(△P)3の状態の数は 4πP2dp/(△P)3=4πP2dp△V/h3
電子はスピン 1/2 で、各運動量状態には二つのスピン状態(”上向き”と”下向き”)がある。 従って状態の数は二倍になる。
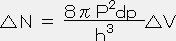 個の状態があり、それが体積△Vの領域にあって、PとP+dpの間の運動量を持つ事の出来る電子の最大の数である。上の式を積分すると
個の状態があり、それが体積△Vの領域にあって、PとP+dpの間の運動量を持つ事の出来る電子の最大の数である。上の式を積分すると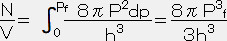 ,
, 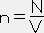 とおくと(nは粒子数密度)
◆
とおくと(nは粒子数密度)
◆ 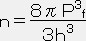 ,
, 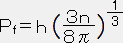 ・・・・・ (26)
フェルミ運動量(=Pf)は粒子の質量ではなくて、単位体積当たりの粒子数(=粒子数密度)に依存している事が分る。
・・・・・ (26)
フェルミ運動量(=Pf)は粒子の質量ではなくて、単位体積当たりの粒子数(=粒子数密度)に依存している事が分る。電子の質量をmとすると、1個の電子は相対論的エネルギー E=(P2+m2)1/2 をもっている。そうした気体中では全エネルギー ETOTAL は
ETOTAL=NxE=V
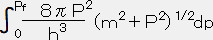 全エネルギー密度 ρ は
全エネルギー密度 ρ は◆ ρ=ETOTAL/V=
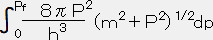 ・・・・・ (27)
ETOTALをVで微分すると
・・・・・ (27)
ETOTALをVで微分するとdETOTAL/dV=V
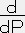 (
(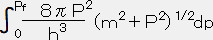 )
) 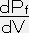 +
+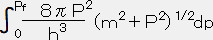
=V
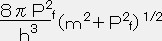
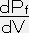 +ρ
今扱っている系は閉じた系だから、圧力Pは熱力学の第一法則で△Qをゼロにして求める事が出来る。
+ρ
今扱っている系は閉じた系だから、圧力Pは熱力学の第一法則で△Qをゼロにして求める事が出来る。P=dETOTAL/dV=ーV
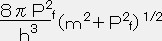
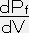 ーρ
ーρ
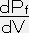 =
=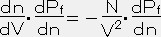 ,
, 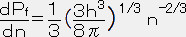 だから V
だから V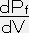 =ーPf/3 従って
P=
=ーPf/3 従って
P=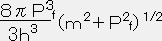 ーρ
が得られる。気体が狭い空間に押し込められると気体は相対論的になる。その結果 Pf≫m となるので、(27)と上の式は
ーρ
が得られる。気体が狭い空間に押し込められると気体は相対論的になる。その結果 Pf≫m となるので、(27)と上の式は◆ ρ

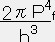 , P
, P 
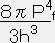 ーρ ・・・・・ (28)
上の二つの式より、下記の式が成り立つ。
ーρ ・・・・・ (28)
上の二つの式より、下記の式が成り立つ。◆ P

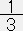 ρ ・・・・・ (29)
これらの具体例は付録6:フェルミ縮退した気体の諸量の計算を参照
ρ ・・・・・ (29)
これらの具体例は付録6:フェルミ縮退した気体の諸量の計算を参照
◆ ρ=μmpne ・・・・・ (30) μ=原子核の核子数/電子数(1 or 2程度の値)、mpは陽子の質量(陽子の質量は電子の質量の1836倍だからは陽子の質量を用いる)、neは電子数密度。式(26)、(28)、(29)、(30)より次の式が成り立つ。(Pは圧力)
◆ P=kρ4/3 , k=
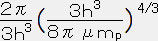 =151.316 m2/3 ・・・・・ (31)
ニュートン的な星の構造を決める式は(13)及び(17)である。それらを積分すると
=151.316 m2/3 ・・・・・ (31)
ニュートン的な星の構造を決める式は(13)及び(17)である。それらを積分するとM=4πR3ρ/3 , P=ρM/R 上の二つの式からRを消去すると、M=
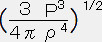 式(31)より、
P3/ρ4=k3だから
∴ M=
式(31)より、
P3/ρ4=k3だから
∴ M=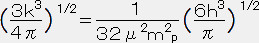 距離化単位で、μ=1としてMを計算すると
距離化単位で、μ=1としてMを計算するとM=1.87x103m=1.27Ms (Ms:太陽の質量=1.477x103m) この値は、重力が冷たい非相対論的な原子核気体に起因している時、相対論的な電子気体で支え得る最大質量の大体の目安を与えている。この値をチャンドラセカール限界質量と呼ぶ。この値より重い星は電子の圧力では支えきれず、白色矮星にはなり得ない。白色矮星と連星をなす伴星からのガス吸収により質量がチャンドラセカール限界をを超えると、超新星爆発を起こし超新星になるか、中性子星になると考えられている。
gα'β'=Λαα'Λββ'ηαβ Λαα'(又はΛββ')は変換行列である。
Λαα'=∂xα/∂xα' (xα=t,x,y,z xα'=t,r,θ,φ)
X=rsinθcosφ , Y=rsinθsinφ , Z=rcosθ
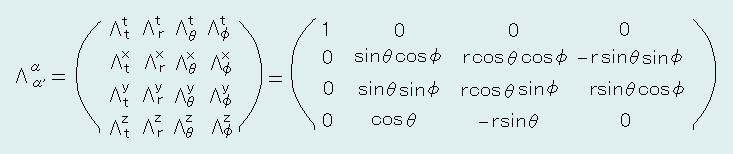
α≠βなら、ηαβ=0 だから α=β だけを計算すれば良い。 gα'β'=Λαα'Λαβ'ηαα
gtt=(Λtt)2η00+(Λxt)2+(Λyt)2+(Λzt)2=-1
grr=(Λtr)2+(Λxr)2+(Λyr)2+(Λzr)2=sin2θcos2φ+sin2θsin2φ+cos2θ=1
gθθ=(Λtθ)2+(Λxθ)2+(Λyθ)2+(Λzθ)2=r2cos2θcos2φ+r2cos2θsin2φ+r2sin2θ=r2
gφφ=(Λtφ)2+(Λxφ)2+(Λyφ)2+(Λzφ)2=r2sin2θsin2φ+r2sin2θcos2φ=r2sin2θ
gtr=gtθ=gtφ=grt=gθt=gφt=0 , grθ=grφ=gθr=gφr=0 , gθφ=gφθ=0
ds2=gα'β'dxα'dxβ' であるから故に
ds2=ーdt2+dr2+r2(dθ2+sin2θdφ2)
ds2=-dτ2=gαβdxαdxβ となる(特殊相対論入門 6.時間の遅れと固有時間と曲線座標系 4. メトリックテンソルを参照)。従って固有時間 dτ は dτ=
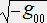 dt になる。時空が平坦な場合、g00=-1 なので dτ=dt
dt になる。時空が平坦な場合、g00=-1 なので dτ=dt
シュワルツシルトの外部解では g00=-(1ー2M/r) だから、g00≧-1 (-g00≦1) r(=動径)が小さいか又はM(=質量)が大きい時、つまり重力場が強い時 -g00 は0に近づくので、dτ≦dt となり、重力場が強いと時間の進み具合が、時空が平坦な場合に比べて遅くなる。
g00 を地球の場合と太陽の場合について計算してみる。
地球の場合、M=4.435x10-3m(距離化単位 SI単位の場合:5.973x1024Kg) r=6.731x106m → g00=-1+1.39x10-9
太陽の場合 g00=-1+4.244x10-6
となり、両者とも時間の遅れは殆んど感じられない。
ブラックホールになるのは(r<2M)、地球の場合、半径が0.9cm、太陽の場合3Kmである。
地球の半径が1.2cmになったら、g00=-0.2608、dτ=0.5dt が導かれ、地球上の時間の経過は平坦な時空の時間の経過に比べ半分になる。
N0:音源が静止いる時の振動数
λ0:音源が静止いる時の波長 ( λ0 =V/N0)
λ:音源が速度vで運動している時の波長 ( λ=(Vーv)/N0 )
N:速度uで運動している観測者が受け取る振動数
とすると、音のドップラー効果は N=
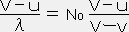 ( v > u なら高く聞こえ、v < u なら低く聞こえる )
( v > u なら高く聞こえ、v < u なら低く聞こえる )
系Oでの光子の四元運動量は (E,Ecosθ,Esinθ,0) である。系O'での光子の四元運動量の第0成分をE'とすると、速度vのローレンツ変換によりE'は
E'=(EーvEcosθー0・Esinθ)/
 E=hν , E'=hν' (hはプランク定数) の関係があるので
E=hν , E'=hν' (hはプランク定数) の関係があるのでν'=ν(1ーvcosθ)/
 が成り立つ。θの値が
が成り立つ。θの値がν'=ν(1ーv)/
 ν'<νとなり、光子の振動数が減り(=波長が長くなる)、赤方偏移が起こる
・ θ=π(光源が近づいている)の時
ν'<νとなり、光子の振動数が減り(=波長が長くなる)、赤方偏移が起こる
・ θ=π(光源が近づいている)の時ν'=ν(1+v)/
 ν'>νとなり、光子の振動数が増え(=波長が短くなる)、青方偏移が起こる
・ θ=π/2(光子の運動が観測者に対して垂直)の時
ν'>νとなり、光子の振動数が増え(=波長が短くなる)、青方偏移が起こる
・ θ=π/2(光子の運動が観測者に対して垂直)の時ν'=ν/
 音の場合、波が横から来る時はドップラー効果は生じない。しかし光の場合には、上の式で分かる様に、相対論に特有な横ドップラー効果が生じる。これを横ドップラー偏移といい、時間ののびのために起こる。
音の場合、波が横から来る時はドップラー効果は生じない。しかし光の場合には、上の式で分かる様に、相対論に特有な横ドップラー効果が生じる。これを横ドップラー偏移といい、時間ののびのために起こる。
z=
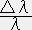 =
= 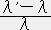 =
= 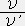 -1
λ ,ν : 星の中心からr1だけ離れた点Pで、放出された光子の波長と振動数
λ' ,ν' : 星の中心からr2だけ離れた点Qでの、点Pで放出された光子の波長と振動数
-1
λ ,ν : 星の中心からr1だけ離れた点Pで、放出された光子の波長と振動数
λ' ,ν' : 星の中心からr2だけ離れた点Qでの、点Pで放出された光子の波長と振動数
第三等号の右辺は λν=λ'ν'=1(=光速) より導かれる。
重力赤方偏移の現象は二つの方法で説明が付く。一つは光子が重力に逆らって運動しているのでエネルギーが減少し赤方偏移が起こる。二つ目は、二つの地点の重力の強さの違いでの、固有時間の違いによるものである。(付録2:重力による時間の遅れを参照) ・ エネルギー減少による説明
E'=E-m(ψ(Q)ーψ(P)) , E:点Pでの粒子のエネルギー , E':点Qでの粒子のエネルギー
ψ(P):点Pでの重力ポテンシャル , ψ(Q):点Qでの重力ポテンシャル (ψ(P)>ψ(Q)) ψ(Q)ーψ(P)=
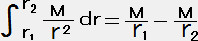 点Qが十分遠方であれば、
点Qが十分遠方であれば、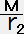
 0
粒子を光子に置き換えると
0
粒子を光子に置き換えるとE=hν , E'=hν' (hはプランク定数) , m=E=hν (物質とエネルギーは等価のため) の関係があるので
hν'=hν-hν(ψ(Q)ーψ(P))

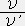 =
= 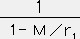 1-M/r1 < 1 なので、ν>ν'となり点Qで赤方偏移が起こる。
1-M/r1 < 1 なので、ν>ν'となり点Qで赤方偏移が起こる。r1 》 M の時、1-M/r1

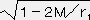 なので (普通の星では十分に成り立つ。下記の註を参照)
なので (普通の星では十分に成り立つ。下記の註を参照)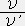 =
= 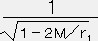 シュワルツシルトの外部解に於ける式(15)と静的で球対称的な星のメトリックに於ける式(2)より
シュワルツシルトの外部解に於ける式(15)と静的で球対称的な星のメトリックに於ける式(2)より1-2M/r1 = e2φ 故に光子の赤方偏移の量 z は
z =
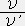 -1 = e-φ-1
-1 = e-φ-1註
太陽及び地球の質量 1.477x103m , 4.435x10-3m (距離化単位)
太陽及び地球の半径 6.960x108m , 6.371x106m
dτ =
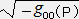 dt , dτ' =
dt , dτ' = 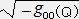 dt (付録2:重力による時間の遅れを参照)
振動数は1秒間に何回振動したという量であるから、時空が平坦な系の光の振動数Nを基準とすると、固有時間dτの系の振動数はN/dτ回となる。従って
dt (付録2:重力による時間の遅れを参照)
振動数は1秒間に何回振動したという量であるから、時空が平坦な系の光の振動数Nを基準とすると、固有時間dτの系の振動数はN/dτ回となる。従って
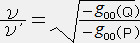 Pの方がQより重力が強いので、dτ<dτ' (
Pの方がQより重力が強いので、dτ<dτ' ( 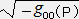 <
< 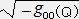 )
)従ってν>ν'となり点Qで赤方偏移が起こる。 Qが十分遠方であれば、
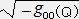 =1になり、
=1になり、ν'=
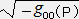 ν=νeφ (λ=
ν=νeφ (λ=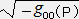 λ'=λ'eφ)
λ'=λ'eφ)( ∵ 静的で球対称的な星のメトリックに於ける式(2)より
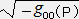 = eφだから )
故に光子の赤方偏移の量 z は
= eφだから )
故に光子の赤方偏移の量 z はz =
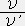 -1 = e-φ-1
Qが遠方でない時の赤方偏移の量は
-1 = e-φ-1
Qが遠方でない時の赤方偏移の量は  と ーg00=e2φ より求まる。
と ーg00=e2φ より求まる。
(P:圧力、ρ:密度、C:任意の定数、n:ポリトロープ指数)
球対称で静水圧平衡が成り立つ様な系では、圧力勾配による外向きの力と、万有引力による内向きの力が釣り合うので
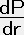 =ー
=ー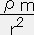 m:半径rの球の中に含まれる質量
m:半径rの球の中に含まれる質量
が成立する。
上の式に r2 を掛け、r で微分すると
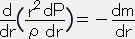 =ー4πr2ρ
=ー4πr2ρ
ポリトロープの質量密度ρと圧力Pの関係式で、 P=Cρ2(ポリトロープ指数nを1とする) を仮定すると
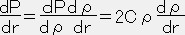 なので
なので
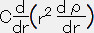 +2πr2ρ=0
+2πr2ρ=0 
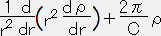 =0
=0
ρ=12(P*P)1/2 と P=Cρ2より C=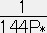 、A2=
、A2=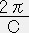 =288P*π とおくと、上の式は
=288P*π とおくと、上の式は
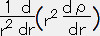 +A2ρ=0
+A2ρ=0 
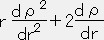 +A2ρr=0
上の微分方程式の解は ρ=α
+A2ρr=0
上の微分方程式の解は ρ=α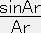 である。星の中心では
である。星の中心では 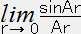 =1 なので、α=ρc(星の中心の質量密度)
=1 なので、α=ρc(星の中心の質量密度)∴ ρ=ρc
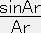 , P=ρ2/(144P*)=Cρ2
次に星の半径と全質量を求める。星の表面では密度ρが0になるから、sinAr=0 → r=π/A
∴ 星の半径 R=π/A=
, P=ρ2/(144P*)=Cρ2
次に星の半径と全質量を求める。星の表面では密度ρが0になるから、sinAr=0 → r=π/A
∴ 星の半径 R=π/A=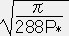 =
=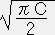
星の全質量Mは
M=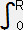 4πρr2dr=4πρc
4πρr2dr=4πρc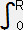
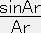 r2dr=
r2dr=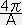 ρc
ρc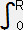 rsinArdr
rsinArdr
∫rsinArdr=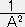 sinArー
sinArー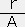 cosAr だから
cosAr だから
半径rの質量mは
m=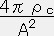 (sinAr/AーrcosAr)
(sinAr/AーrcosAr)
全質量 M は r=R=π/A の時だから、上の式の r にπ/Aを代入して
∴ 星の質量 M= 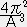 ρc=ρc(2πC3)1/2
ρc=ρc(2πC3)1/2
【例】 電子の粒子数密度より、白色矮星の質量密度、圧力、質量及び半径を求める。
ρc=2x電子の粒子数密度x陽子の質量 になる。(式(30)を参照)
ρc=2x1037x1.242x10-54=2.484x10-17 /m2 (1.242x10-54=陽子の質量)
圧力 Pc は
Pc=151.316x(2.484x10-17)4/3=1.097x10-20 /m2 (151.316=K 式(31)を参照)
ポリトロープの関係式 P=Cρ2 より
C=1.097x10-20/(2.484x10-17)2
星の質量 M は上の式より
M=2.484x10-17x(2πC3)1/2=4.666x103 m
星の半径 R は
R=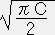 =5.284x106 m
=5.284x106 m
距離化単位をSI単位に変換して表にまとめると
|
①太陽のような星
M=4πR3ρ/3より、質量密度が分かる。それらから式(23)又は(24)により圧力が分かる。それらを計算すると
質量密度ρ=1.046x10-24/m2 , 圧力P=1.110x10-30/m2
③質量が太陽と同じで、半径が10Kmの典型的な中性子星
質量密度ρ=3.526x10-10/m2 , 圧力P=3.730x10-11/m2
質量Mと半径Rは②と同じ方法で求まる。
質量密度ρ=2.484x10-17/m2 , 圧力P=1.097x10-20/m2
質量M=2.566x103m , 半径R=2.911x106m
|
Ⅰ.粒子数密度
Ⅱ.フェルミ運動量
Ⅲ.フェルミ速度
Ⅳ.フェルミエネルギー(非相対論的)
Ⅴ.フェルミ温度
Ⅵ.フェルミエネルギー(相対論的)
Ⅶ.気体の全エネルギー密度
付録5の②~④の星に対する,上記の計算結果を表にまとめると
|
|